Chapter 10

Coupled Prediction: Integrating Atmosphere-Wave-Ocean forecasting

CHAPTER
COORDINATORS

John Siddorn

CHAPTER
AUTHORS

Natacha B. Bernier, Øyvind Breivik, Kai H. Christensen, Stephen G. Penny, and Keguang Wang

10.2 Coupling processes

10.2.1 Waves and their role in air-sea exchange

Waves have been called the gearbox of the climate system (Semedo et al., 2011). The analogy highlights the mediating role of the wave field between the atmosphere and the ocean interior. It may seem surprising that the sea surface demands its own class of numerical model. The other components (atmosphere, ocean, sea ice, land surface) have real substance, i.e. they each represent a three-dimensional chunk of the Earth system. In contrast, the wave model is a representation of a surface between two media, namely the air and the sea (Figure 10.4). There are, however, good practical reasons for this split. If we had access to unlimited computing power, we could model the ocean and the atmosphere with a grid resolution approaching Kolmogorov’s microscale. That would mean that the Navier Stokes equations could be solved in the approximative limit known as DNS (Moin and Mahesh, 1998). In this case, the (liquid) ocean would presumably interact with the (gaseous) atmosphere and on their interface would form a wavy surface that, given a sufficiently strong momentum flux (mostly from the atmosphere to the ocean), would form droplets and bubbles as the waves start to break. The computational reality is far from this. At present, we can model the ocean and the atmosphere with models that have grid cells of tens of metres in the horizontal if we limit ourselves to small domains, whereas the waves that form under the influence of the wind have wavelengths of the order of some metres to hundreds of metres and so cannot be explicitly resolved together with the bulk ocean properties.

The behaviour of these waves determines the mass and momentum fluxes between the ocean and the atmosphere. As waves grow under the influence of the wind, they become steeper. In this phase they are also choppier than they will be later on. All this means that the momentum flux between the atmosphere and the ocean is affected by the presence of waves (Janssen et al., 2004; Breivik et al., 2015). There is also very important feedback between the waves and the atmosphere. As waves grow, the sea surface becomes rougher, slowing the near-surface winds and increasing the momentum flux from the atmosphere to the wave field. This has the effect of stemming the deepening of low-pressure systems. This is important in the formation and growth of extratropical lows (Janssen, 1991 and 2004), but also in the evolution of tropical cyclones (discussed further below).

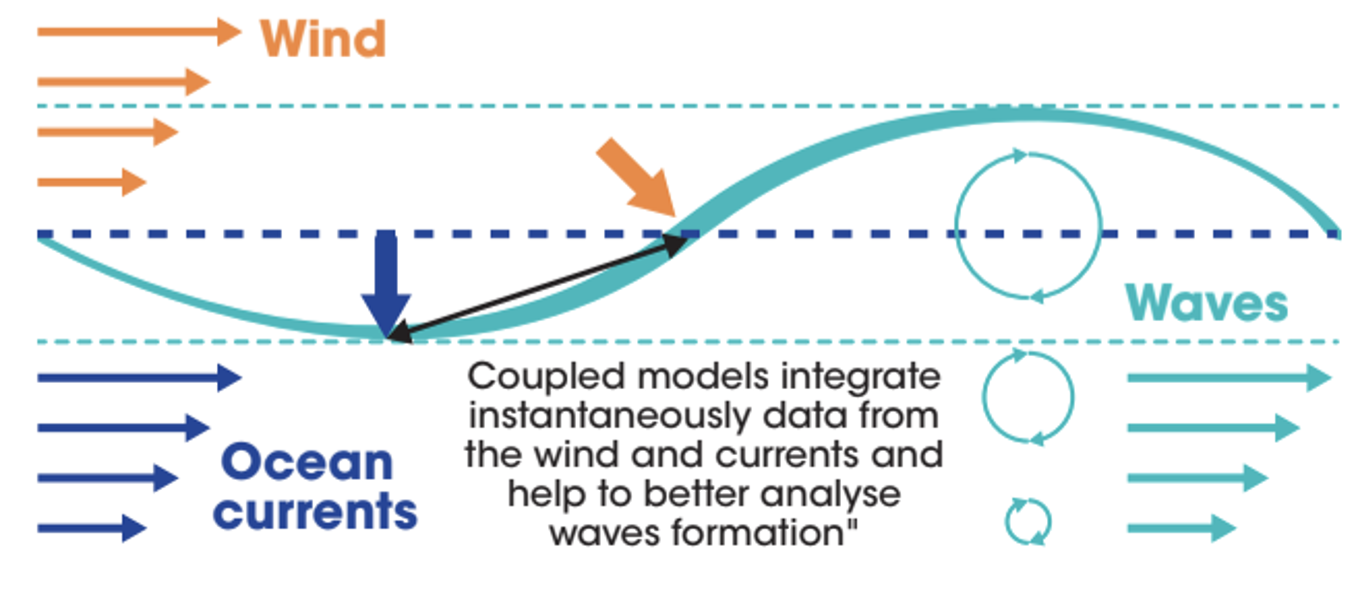
Figure 10.4. Representation of AWO coupled models.

A secondary effect of waves on the air-sea interaction is through their ability to impart momentum and turbulent kinetic energy to the ocean interior(Figure 10.4). As waves grow, they absorb momentum that would otherwise go directly to the formation of ocean currents. As waves break, they part with this momentum, and also inject turbulent kinetic energy into the ocean (Janssen et al., 2004; Rascle et al., 2006; Ardhuin et al., 2008 and 2009). This leads to a redistribution of momentum and kinetic energy in time and space (Ardhuin and Jenkins, 2006; Breivik et al., 2015; Staneva et al., 2017; Wu et al., 2019), and has a profound effect on near-shore processes (Uchiyama et al., 2010; Kumar et al., 2012) where waves interact strongly with the currents. It is also clear that in open ocean conditions the mixed-layer depth is a function of the wave activity, in part sustained by the Langmuir turbulence (McWilliams et al., 1997; Fan and Griffies, 2014; Li et al., 2016 and 2017; Li and Fox-Kemper, 2017; Ali et al., 2019). The enhanced mixing due to waves is thus important for the sea surface temperature, which helps to determine the air-sea heat flux and thus constitutes an important feedback mechanism between the atmosphere and the ocean.

10.2.2 Land/sea exchanges

Land-sea interactions take place on a wide range of spatial and temporal scales. The presence of land modifies the weather in the coastal zone, e.g. the daily variations in wind speed and direction due to the sea breeze, and hence the atmosphere provides an indirect link between the land and the ocean. Another example of this indirect coupling is the way large-scale weather systems can influence the transport pathways of river water (Osadchiev et al., 2020).

The physical couplings between land, ocean, and atmosphere are not necessarily equal in strength and importance, and we often observed a lagged response. The runoff from rivers is dependent on the precipitation over a potentially very large catchment area, with significant lag between specific precipitation events and the freshwater discharge to the coastal ocean. This lag is particularly pronounced in temperate and polar regions where the precipitation accumulates as snow during parts of the year. This is reflected by the state-of-the-art of coupled modelling, as very few systems couple the ocean to the land, but rather use the atmosphere as a mediator.

10.2.3 Air-sea exchanges across sea ice

At high latitudes, air-sea exchange is modified by the presence of sea ice. Varying in thickness up to a couple of metres, sea ice is sensitive to forcing from both air and sea and the air, sea, and sea ice are strongly coupled. Geophysical scale sea ice is essentially a mixture of ice floes of varying size and thickness, with the added complexity of being rafted and ridged. Describing accurately the sea ice mechanical behaviour is extremely challenging, although modelling sea ice as plastic materials at the large scale has long been a successful approach (Coon et al., 1974; Hibler, 1979; Hunke and Dukwicz, 1997; Girard et al., 2011). In medium to high model resolutions (≤ 10km), such models can generate small-scale features such as the ice leads (Hutchings et al., 2005; Wang and Wang, 2009; Girard et al., 2011; Spreen et al., 2017). This thin ice cover has a very small heat content and easily melts away during summer, resulting in large seasonal variations of sea ice extent.

In much of the pack ice region, the thermodynamic and dynamic interactions between air and sea are greatly suppressed. During wintertime, the air-sea heat flux through leads is two orders of magnitude larger than that through thick ice (Maykut, 1978). Dynamically, pack ice behaves as a low-pass filter, the air and sea surface stresses act on the ice cover thus driving the advection and deformation of sea ice, while ocean waves are generally suppressed. The MIZ is a highly complex region consisting of ice floes of varying dimensions and shapes. Wave energy propagating into the MIZ can lead to rapid breakup. The damping of waves in sea ice is directly related to the amount of energy imparted on the sea ice. This is a field of active research, and it is presently not fully clear how the MIZ attenuates wave energy (Doble and Bidlot, 2013; Williams et al., 2013; Kohout et al., 2014; Sutherland and Rabault, 2016; Ardhuin et al., 2016; Rabault et al., 2020).

Landfast ice is a special region where the air-sea interaction nearly ceases. It generally appears in winter seasons and often occurs in shallow waters where ridged ice grounds on the seabed (Mahoney et al., 2014), or occurs where islands are close to each other (Divine et al., 2003). Modelling studies have shown that adding base stress due to grounding ridges and increasing ice tensile strength improve the simulation of landfast ice evolution (Lemieux et al., 2016), although in some Arctic shelf seas the time duration needs to be further improved.

In coupled modelling, a key consideration is whether to couple the sea ice directly to the atmosphere or only through the ocean model. In some recent coupled models, particularly for high-resolution short-term atmosphere, ocean, and sea ice forecasts, the timestep for coupling has decreased to one hour or less, e.g. the coupled ocean-ice model METROMS at the Norwegian Meteorological Institute (Naughten et al., 2018), or the atmosphere-ice coupled model at UKMO (Ridley et al., 2018). In these cases, the difference between using the atmosphere timestep or ocean timestep is generally negligible.

10.2.4 The importance of air-sea exchanges during storms and other extreme events

Air-sea exchange really comes to the fore in the development of tropical cyclones. The sea surface temperature must as a general rule exceed 26.5ºC to sustain the growth of the cyclone (Emanuel, 1986). However, the depth to which the ocean’s temperature must be above this critical threshold is also important. As the cyclone moves across the sea surface, the Ekman transport will lead to divergence, and vertical Ekman pumping will eventually lead cooler water to the surface. If the cyclone is moving sufficiently slowly, this will eventually kill the cyclone (Mogensen et al, 2017). Thus, it is essential to include an ocean model component that responds to the atmospheric forcing.

Polar lows are of a decidedly less extreme nature than tropical cyclones, but they share the same dependence on sea surface temperature (Rasmussen and Turner, 2003). As winds blow off the sea ice, the air is rapidly warmed by the (relatively) warm ocean surface. Under the appropriate atmospheric conditions (Kolstad, 2015), this can lead to the formation of polar lows. These are small-scale, intense cyclones, typically with gale-force winds. If the cyclone is rather stationary, a shallow layer of warmer water can mix with cooler waters through Ekman pumping. As the ocean temperature is key to sustaining a cyclone, the water mixing can sometimes be enough to inhibit further growth of the polar low.

Examples of instantaneous coupling between land, ocean, and atmosphere also include coastal inundation during landfall of tropical cyclones (Lee et al., 2019). In these cases, heavy precipitation leads to a swelling of local rivers, which is often coincidental with a large storm surge. The result is a rapid sea-level rise that may cause extensive damage to coastal infrastructure, especially when combined with large surface waves and strong winds.

Previous section Next section

References

Ali, A., Christensen, K., Breivik, O., Malila, M., Raj, R., Bertino, L., Chassignet, E., Bakhoday-Paskyabi M. (2019). A comparison of Langmuir turbulence parameterizations and key wave effects in a numerical model of the North Atlantic and Arctic Oceans. Ocean Modelling,137, pp 76-97, https://doi.org/10.1016/j.ocemod.2019.02.005

Allard, R. A., Campbell, T. J. , Smith, T. A., Jensen, T. G., Chen, S., Cummings, J. A., Chen, S., Doyle, J., Xiaodong, H., Small, R.J., Carrol, S.N. (2010). Validation Test Report for the Coupled Ocean Atmosphere Mesoscale Prediction System (COAMPS) Version 5.0 NRL/MR/7322–10-9283. Stennis Space Center, MS: Oceanography Division, Naval Research Laboratory, 172 pp.

Allard, R. A., Travis, A. S., Jensen, T. G., Chu, P. Y., Rogers, E., and Campell, T. J. (2012). Validation Test Report for the Coupled Ocean / Atmosphere Mesoscale Prediction System (COAMPS) Version 5.0: Ocean / Wave Component Validation. Naval Research Lab Tech Report, (NRL/MR/7320--12-9423).

Ardhuin, F., Rascle, N., Belibassakis, K. (2008). Explicit wave-averaged primitive equations using a generalized Lagrangian mean. Ocean Modelling, 20(1), 35-60, https://doi.org/10.1016/j.ocemod.2007.07.001

Ardhuin, F., Marie, L., Rascle, N., Forget, P., Roland, A. (2009). Observation and estimation of Lagrangian, Stokes and Eulerian currents induced by wind and waves at the sea surface. Journal of Physical Oceanography, 39, 2820-2838, https://doi.org/10.1175/2009JPO4169.1

Ardhuin, F., and Jenkins A., (2006). On the Interaction of Surface Waves and Upper Ocean Turbulence. Journal of Physical Oceanography, 36, 551-557, https://doi.org/10.1175/JPO2862.1

Ardhuin, F., Sutherland, P., Doble, M., Wadhams, P. (2016). Ocean waves across the Arctic: Attenuation due to dissipation dominates over scattering for periods longer than 19 s. Geophysical Research Letters, 43(11), 5775-5783, https://doi.org/10.1002/2016GL068204

Ardhuin, F., Gille, S. T., Menemenlis, D., Rocha, C. B., Rascle, N., Chapron, B., Gula, J., Molemaker, J. (2017). Small-scale open ocean currents have large effects on wind wave heights. Journal of Geophysical Research: Oceans, 122(6), 4500–4517. https://doi.org/10.1002/2016JC012413

Barker, C. H., Kourafalou, V. H., Beegle-Krause, C. J., Boufadel, M., Bourassa, M. A., Buschang, S. G., Androulidakis, Y., Chassignet, E.P., Dagestad, K.-F., Danmeier, D.G., Dissanayake, A.L., Galt, J.A., Jacobs, G., Marcotte, G., Özgökmen, T., Pinardi, N., Schiller, R.V., Socolofsky, S.A., Thrift-Viveros, D., D., Zhang, A., Zheng, Y. (2020). Progress in operational modeling in support of oil spill response. Journal of Marine Science and Engineering, 8(9), 1-55, https://doi.org/10.3390/jmse8090668

Belcher, S.E., Hewitt, H.T., Beljaars, A., Brun, E., Fox-Kemper, B., Lemieux, J.F., Smith, G., and Valcke, S. (2015). Ocean-Waves-Sea Ice- Atmosphere Interactions. In: Brunet, G., Jones, S. and Ruti, P. (eds.) “Seamless prediction of the Earth system: from minutes to months”, WMO, 1156. World Meteorological Organisation, Geneva, pp. 155-170.

Bender, M. A., and Ginis, I. (2000). Real-Case Simulations of Hurricane–Ocean Interaction Using A High-Resolution Coupled Model: Effects on Hurricane Intensity. Monthly Weather Review, 128(4), 917-946, https://doi.org/10.1175/1520-0493(2000)128<0917:RCSOHO>2.0.CO;2

Bernie, D. J., Guilyardi, E., Madec, G., Slingo, J. M., Woolnough, S. J., and Cole, J. (2008). Impact of resolving the diurnal cycle in an ocean-atmosphere GCM. Part 2: A diurnally coupled CGCM. Climate Dynamics, 31(7-8), 909-925, https://doi.org/10.1007/s00382-008-0429-z

Brassington, G. B., Martin, M. J., Tolman, H. L., Akella, S., Balmeseda, M., Chambers, C. R. S., Chassignet, T., Cummings, J.A., Drillet, Y., Jansen, P.A.E.M., Laloyaux, P., Lea, D., Mehra, A., Mirouze, I., Ritchie, H., Samson, G., Sandery, P.A., Smith, G.C., Suarez, M., and Todling, R. (2015). Progress and challenges in short- to medium-range coupled prediction. Journal of Operational Oceanography, 8, s239-s258, https://doi.org/10.1080/1755876x.2015.1049875

Breivik, Ø., Mogensen, K., Bidlot, J.-R., Balmaseda, M.A., Janssen, P.A. (2015). Surface Wave Effects in the NEMO Ocean Model: Forced and Coupled Experiments. Journal of Geophysical Research: Oceans, 120, 2973-2992, https://doi.org/10.1002/2014JC010565

Brunet, G., Keenan, T., Onvlee, J., Béland, M., Parsons, D., and Mailhot, J. (2010). The next generation of regional prediction systems forweather,water and environmental applications. CAS XV Vision paper(Agenda item 8.2).

Coon, M. D., Maykut, G. A., Pritchard, R. S., Rothrock, D. A., and Thorndike A. S. (1974). Modeling the pack ice as an elastic-plastic material. AIDJEX Bull. 24, pp. 1-106, Univ. of Wash., Seattle, Washington.

Davidson, F.J.M., Allen, A., Brassington, G.B., Breivik, Ø., Daniel, P., Kamachi, M., Sato, S., King, B., Lefevre, F., Sutton, M., and Kaneko, H. (2009). Applications of GODAE ocean current forecasts to search and rescue and ship routing. Oceanography, 22(3), 176-181, https://doi.org/10.5670/oceanog.2009.76

Divine, D., Korsnes, R., and Makshtas, A. P. (2003). Variability and climate sensitivity of fast ice extent in the north-eastern Kara Sea. Polar Research, 22, 27-34, https://doi.org/10.3402/polar.v22i1.6440

Doble, M. J., and Bidlot, J.-R. (2013). Wave buoy measurements at the Antarctic sea ice edge compared with an enhanced ECMWF WAM: Progress towards global waves-in-ice modelling. Ocean Modelling, 70, 166-173, https://doi.org/10.1016/j.ocemod.2013.05.012

Dzwonkowski, B., Greer, A.T., Briseno-Avena, C., Krause, J.W., Soto, I.M., Hernandez, F.J., Deary, A.L., Wiggert, J.D., Joung, D., Fitzpatrick, P.J., O’Brien, S.J., Dykstra, S.L., Lau, Y., Cambazoglu, M.K., Lockridge, G., Howden, S.D.,

Shiller, A.M., Graham, W.M. (2017). Estuarine influence on biogeochemical properties of the Alabama shelf during the fall season. Continental Shelf Research, 140, 96-109, https://doi.org/10.1016/j.csr.2017.05.001

Emanuel,K.A.(1986).AnAir-SeaInteractionTheory for TropicalCyclones.PartI:Steady-StateMaintenance.Journal of the Atmospheric Sciences, 43(6), 585-605, https://doi.org/10.1175/1520-0469(1986)043<0585:AASITF>2.0.CO;2

Fan, Y., Ginis, I., and Hara, T. (2009). The effect of wind-wave-current interaction on air-sea momentum fluxes and ocean response in tropical cyclones. Journal of Physical Oceanography, 39(4), 1019-1034, https://doi.org/10.1175/2008JPO4066.1

Fan, Y., and Griffies, S.M. (2014). Impacts of parameterized Langmuirturbulence and non-breakingwave mixing in global climate simulations. Journal of Climate, 27, 4752-4775, https://doi.org/10.1175/JCLI-D-13-00583.1

Fu, L.L. (2007). Intraseasonal variability ofthe equatorial Indian ocean observed from sea surface height,wind, and temperature data. Journal of Physical Oceanography, 37(2),188-202, https://doi.org/10.1175/JPO3006.1

Girard, L., Bouillon, S., Weiss, J., Amitrano, D., Fichefet, T., and Legat, V. (2011). A new modeling framework for sea-ice mechanics based on elasto-brittle rheology. Annals of Glaciology, 52(57), 123-132, https://doi.org/10.3189/172756411795931499

Guiavarc’h, C., Roberts-Jones, J., Harris, C., Lea, D. J., Ryan, A., and Ascione, I. (2019). Assessment of ocean analysis and forecast from an atmosphere–ocean coupled data assimilation operational system. Ocean Science, 15(5), 1307-1326, https://doi.org/10.5194/os-15-1307-2019

Harlim, J., Oczkowski, M., Yorke, J. A., Kalnay, E., and Hunt, B.R. (2005). Convex Error Growth Patterns in a Global Weather Model. Physical Review Letters, 94, 228501, https://doi.org/10.1103/PhysRevLett.94.228501

Hibler, W. D. III (1979). A dynamic thermodynamic sea ice model. Journal of Physical Oceanography, 9, 815-846, https://doi.org/10.1175/1520-0485(1979)009<0815:ADTSIM>2.0.CO;2

Holbrook, N. J., Scannell, H. A., Sen Gupta, A., Benthuysen, J. A., Feng, M., Oliver, E. C. J., Alexander, L.V., Burrows, M.T., Donat, M.G., Hobday, A.J., Moore, P.J., Perkins-Kirkpatrick, S.E., Smale, D.A., Straub, S.C., Wernberg, T. (2019). A global assessment of marine heatwaves and their drivers. Nature Communications, 10(1), 1-13, https://doi.org/10.1038/s41467-019-10206-z

Hunke, E. C., and Dukowicz, J. K. (1997). An elastic-viscous-plastic model for sea ice dynamics. Journal of Physical Oceanography, 27(9), 1849-1867, https://doi.org/10.1175/1520-0485(1997)027<1849:AEVPMF>2.0.CO;2

Hutchings, J. K., Heil, P., and Hibler, W. D. III (2005). Modeling linear kinematic features in sea ice. Monthly Weather Review, 133, 3481-3497, https://doi.org/10.1175/MWR3045.1

Hyder, P., Edwards, J.M., Allan, R., Hewitt, H.T., Bracegirdle, T.J., Gregory, J.M., Wood, R.A., Meijers, A.J.S., Mulcahy, J., Field, P., Furtado, K., Bodas-Salcedo, A., Williams, K.D., Copsey, D., Josey, S.A., Liu, C., Roberts, C.D., Sanchez, C., Ridley, J., Thorpe, L., Hardiman, S.C., Mayer, M., Berry, D.I., Belcher, S.E. (2018). Critical Southern Ocean climate model biases traced to atmospheric model cloud errors. Nature Communications, 9, 3625, https://doi.org/10.1038/s41467-018-05634-2

Jacox, M. G. (2019). Marine heatwaves in a changing climate. Nature, 571, 485-487. https://doi.org/10.1038/d41586-019-02196-1

Janssen, P.A.E.M. (1991). Quasi-linear theory of wind wave generation applied to wave forecasting. Journal of Physical Oceanography, 21, 1631-1642.

Janssen, P. (2004). The interaction of ocean waves and wind. Cambridge University Press, Cambridge, UK.

Janssen, P., Saetra, O., Wettre, C., Hersbach, H., Bidlot, J. (2004). Impact of the sea state on the atmosphere and ocean. Annales Hydrographiques 6e série, 772, 3-23.

Jullien, S., Masson, S., Oerder, V., Samson, G., Colas, F., and Renault, L. (2020). Impact of ocean-atmosphere current feedback on ocean mesoscale activity: Regional variations and sensitivity to model resolution. Journal of Climate, 33(7), 2585-2602, https://doi.org/10.1175/JCLI-D-19-0484.1

Jung, T., and Vitart, F. (2006). Short-Range and Medium-Range Weather Forecasting in the Extratropics during Wintertime with and without an Interactive Ocean. Monthly Weather Review, 134(7), 1972-1986, https://doi.org/10.1175/MWR3206.1

Kim, H. M., Webster, P. J., and Curry, J. A. (2012). Seasonal prediction skill of ECMWF System 4 and NCEP CFSv2 retrospective forecast for the Northern Hemisphere Winter. Climate Dynamics, 39(12), 2957-2973, https://doi.org/10.1007/s00382-012-1364-6

Kohout, A., Williams, M.J.M., Dean, S.M., Meylan, M.H. (2014). Storm-induced sea-ice breakup and the implications for ice extent. Nature, 509(7502), 604-607, https://doi.org/10.1038/nature13262

Kolstad, E. (2015). Extreme small-scale wind episodes over the Barents Sea: When, where and why? Climate Dynamics, 1-14, https://doi.org/10.1007/s00382-014-2462-4

Kumar, N., Voulgaris, G., Warner, J.C., Olabarrieta, M. (2012). Implementation of the vortex force formalism in the coupled ocean-atmosphere-wave-sediment transport (COAWST) modeling system for inner shelf and surf zone applications. Ocean Modelling, 47, 65-95, https://doi.org/10.1016/j.ocemod.2012.01.003

Laloyaux, P., de Boisseson, E., Balmaseda, M., Bidlot, J. R., Broennimann, S., Buizza, R., Dalhgren, P., Dee, D., Haimberger, L., Hersbach, H., Kosaka, Y., Martin, M., Poli, P., Rayner, N., Rustemeier, E., Schepers, D. (2018). CERA-20C: A Coupled Reanalysis of the Twentieth Century. Journal of Advances in Modeling Earth Systems, 10(5), 1172-1195. https://doi.org/10.1029/2018MS001273

Large, W. G., and Yeager, S. G. (2009). The global climatology of an interannually varying air - Sea flux data set. Climate Dynamics, 33(2-3), 341-364, https://doi.org/10.1007/s00382-008-0441-3

Lee, C.,Hwang, S., Do, K., and Son, S. (2019). Increasing flood risk due to riverrunoffin the estuarine area during a storm landfall. Estuarine, Coastal and Shelf Science, 221, 104-118, https://doi.org/10.1016/j.ecss.2019.03.021

Lemarié, F., Samson, G., Redelsperger, J.-L., Giordani, H., Brivoal, T., and Madec, G. (2021). A simplified atmospheric boundary layer model for an improved representation of air-sea interactions in eddying oceanic models: implementation and first evaluation in NEMO(4.0). Geoscientific Model Development,14, 543-572, https://doi.org/10.5194/gmd-14-543-2021

Lemieux, J.-F., Dupont, F., Blain, P., Roy, F., Smith, G. C., and Flato, G. M. (2016). Improving the simulation of landfast ice by combining tensile strength and a parameterization for grounded ridges. Journal of Geophysical Research: Oceans, 121, 7354-7368, https://doi.org/10.1002/2016JC012006

Lewis, H., Mittermaier, M., Mylne, K., Norman, K., Scaife, A., Neal, R., … Pilling, C. (2015). From months to minutes - exploring the value of high-resolution rainfall observation and prediction during the UK winter storms of 2013/2014. Meteorological Applications, 22(1), 90-104, https://doi.org/10.1002/met.1493

Lewis, H. W., Castillo Sanchez, J. M., Siddorn, J., King, R. R., Tonani, M., Saulter, A., Sykes, P., Pequignet, A.C., Weedon, G.P., Palmer, T., Staneva, J., Bricheno, L. (2018). Can wave coupling improve operationalregional ocean forecasts for the North-West European Shelf? Ocean Science,15, 669-690, https://doi.org/10.5194/os-15-669-2019

Lewis, H. W., Castillo Sanchez, J. M., Arnold, A., Fallmann, J., Saulter, A., Graham, J., Bush, M., Siddorn, J., Tamzin, P., Adrian, L., Edwards, J., Bricheno, L.,Martinez-de la Torre, A., Clark, J.(2019). TheUKC3 regional coupled environmental prediction system. Geoscientific Model Development,12(6), 2357-2400, https://doi.org/10.5194/gmd-12-2357-2019

Li, Q., Webb, A., Fox-Kemper, B., Craig, A., Danabasoglu, G., Large, W.G., Vertenstein, M. (2016). Langmuir mixing effects on global climate: WAVEWATCH III in CESM. Ocean Modeling, 103, 145-160, https://doi.org/10.1016/j.ocemod.2015.07.020

Li, Q., and Fox-Kemper, B. (2017). Assessing the Effects of Langmuir Turbulence on the Entrainment Buoyancy Flux in the Ocean Surface Boundary Layer. Journal of Physical Oceanography, 47(12), 2863-2886, https://doi.org/10.1175/JPO-D-17-0085.1

Li, Q., Fox-Kemper, B., Breivik, O., Webb, A. (2017). Statistical Models of Global Langmuir Mixing. Ocean Modelling, 113, 95-114, https://doi.org/10.1016/j.ocemod.2017.03.016

Lorenz, E.N. (1963). Deterministic nonperiodic flow. Journal of the Atmospheric Sciences, 20, 130-141

Lorenz, E.N. (1967). The nature and theory of the general circulation of the atmosphere. World Meteorological Organization, 218. Available at; https://library.wmo.int/doc_num.php?explnum_id=10889

Mahoney, A. R., Eicken, H., Gaylord, A.G., and Gens, R. (2014). Landfast sea ice extent in the Chukchi and Beaufort Seas: The annual cycle and decadal variability. Cold Regions Science and Technology, 103, 41-56, https://doi.org/10.1016/j.coldregions.2014.03.003

Maykut, G. A. (1978). Energy exchange over young sea ice in the central Arctic. Journal of Geophysical Research: Oceans, 83(C7), 3646-3658, https://doi.org/10.1029/JC083iC07p03646

McWilliams, J.C., Sullivan, P.P., and Moeng, C.-H. (1997). Langmuir turbulence in the ocean. Journal of Fluid Mechanics, 334, 1-30, https://doi.org/10.1017/S0022112096004375

Minobe, S., Kuwano-Yoshida, A., Komori, N., Xie, S. P., and Small, R. J. (2008). Influence of the Gulf Stream on the troposphere. Nature, 452(7184), 206-209, https://doi.org/10.1038/nature06690

Mogensen, K. S., Magnusson, L., Bidlot, J-R. (2017). Tropical cyclone sensitivity to ocean coupling in the ECMWF coupled model. Journal of Geophysical Research: Oceans,122(5),43924412, https://doi.org/10.1002/2017JC012753

Moin, P. and Mahesh, K. (1998). Direct numerical simulation: A Tool in Turbulence Research. Annual Review of Fluid Mechanics, 30(1), 539-578, https://doi.org/10.1146/annurev.fluid.30.1.539

Naughten, K. A., Meissner, K. J., Galton-Fenzi, B. K., England, M. H., Timmermann, R., Hellmer, H. H., Hattermann, T., and Debernard, J. B. (2018). Intercomparison of Antarctic ice-shelf, ocean, and sea-ice interactions simulated by MetROMS-iceshelf and FESOM 1.4. Geoscientific Model Development, 11(4), 1257-1292, https://doi.org/10.5194/GMD-11-1257-2018

Neetu, S., Lengaigne, M., Vialard, J., Samson, G., Masson, S., Krishnamohan, K. S., and Suresh, I. (2019). Premonsoon/Postmonsoon Bay of Bengal Tropical Cyclones Intensity: Role of Air Sea Coupling and LargeScale Background State. Geophysical Research Letters, 2019, 46(4), 2149-2157.

Oerder, V., Colas, F., Echevin, V., Masson, S., and Lemarié, F. (2018). Impacts of the Mesoscale Ocean-Atmosphere Coupling on the Peru-Chile Ocean Dynamics: The Current-Induced Wind Stress Modulation. Journal of Geophysical Research: Oceans, 123(2), 812-833, https://doi.org/10.1002/2017JC013294

Osadchiev, A. A., Pisareva,M.N., Spivak, E. A., Shchuka, S. A., andSemiletov, I. P.(2020). Freshwatertransport between the Kara, Laptev, and East-Siberian seas. Scientific Reports,10(1),1-14, https://doi.org/10.1038/s41598-020-70096-w

Pellerin, P., Ritchie, H., Saucier, F. J., Roy, F., Desjardins, S., Valin, M., and Lee, V. (2004). Impact of a twoway coupling between an atmospheric and an ocean-ice model over the Gulf of St. Lawrence. Monthly Weather Review, 132, 1379-1398, https://doi.org/10.1175/1520-0493(2004)132<1379:IOATCB>2.0.CO;2

Penland, C., andMatrosova, L.(1998).PredictionoftropicalAtlantic sea surface temperaturesusing LinearInverse Modeling. Journal of Climate,11, 483-496, https://doi.org/10.1175/1520-0442(1998)011<0483:POTASS>2.0.CO;2

Penland, C., and Sardeshmukh, P. D. (1995). The optimal growth of tropical sea surface temperature anomalies. Journal of Climate, 8, 1999-2024.

Rabault, J., Sutherland, G., Gundersen, O., Jensen, A., Marchenko, A., Breivik, O. (2020). An Open Source, Versatile, Affordable Waves in Ice Instrument for Scientific Measurements in the Polar Regions. Cold Regions Science and Technology, 170, 11, https://doi.org/10.1016/j.coldregions.2019.102955

Rascle, N., Ardhuin, F., Terray, E. (2006). Drift and mixing under the ocean surface: A coherent one-dimensional description with application to unstratified conditions. Journal of Geophysical Research, 111(C3), 16, https://doi.org/10.1029/2005JC003004

Rasmussen, E.A., Turner (2003). Polar lows: mesoscale weather systems in the polar regions, Cambridge University Press.

Renault, L., Molemaker, M. J., Gula, J., Masson, S., and McWilliams, J. C. (2016) Control and Stabilization of the Gulf Stream by Oceanic Current Interaction with the Atmosphere. Journal of Physical Oceanography, 46, 3439-3453, https://doi.org/10.1175/JPO-D-16-0115.1

Ridley, J. K., Blockley, E.W., Keen, A.B., Rae, J.G.L.,West, A.E., and Schroeder, D. (2018). The sea icemodel component of HadGEM3-GC3.1. Geoscientific Model Development,11(2), 713-723, https://doi.org/10.5194/gmd-11-713-2018

Røed, L.P., and Albretsen, J. (2007). The impact of freshwater discharges on the ocean circulation in the Skagerrak/northern North Sea area Part I: Model validation. Ocean Dynamics, 57(4-5), 269-285, https://doi.org/10.1007/s10236-007-0122-5

Saha, S., Nadiga, S., Thiaw, C., Wang, J., Zhang, Q., Van den Dool, H.M., Pan, H.-L., Moorthi, S., Behringer, D., Stokes, D., Peña, M., Lord, S., White, G., Ebisuzaki, W., Peng, P., Xie, P. (2006). The NCEP Climate Forecast System. Journal of Climate, 19, 3483-3517, https://doi.org/10.1175/JCLI3812.1

Saha, S., Moorthi, S., Pan, H.-L., Wu, X., Wang, J., Nadiga, S., Tripp, P., Kistler, R., Woollen, J., Behringer, D., Liu, H., Stokes, D., Grumbine, R., Gayno, G., Wang, J., Hou, Y.-T., Chuang, H., Juang, H.-M.H., Sela, J., Iredell, M., Treadon, R., Kleist, D., Delst, P.V., Keyser, D., Derber, J., Ek, M., Meng, J., Wei, H., Yang, R., Lord, S., van den Dool, H., Kumar, A., Wang, W., Long, C., Chelliah, M., Xue, Y., Huang, B., Schemm, J.-K., Ebisuzaki, W., Lin, R., Xie, P., Chen, Y., Han, Y., Cucurull, L., Reynolds, R.W., Rutledge, G., Goldberg, M. (2010). The NCEP Climate Forecast System Reanalysis. Bulletin of the American Meteorological Society, 91, 1015-1057, https://doi.org/10.1175/2010BAMS3001.1

Saha, S., Moorthi, S., Wu, X., Wang, J., Nadiga, S., Tripp, P., Behringer, D., Hou, Y.-T., Chuang, H., Iredell, M., Ek, M., Meng,J., Yang,R., PeñaMendez,M., van denDool,H., Zhang,Q.,Wang,W., Chen,M., andBecker, E.(2014). TheNCEP Climate Forecast System Version 2. Journal of Climate, 27, 2185-2208, https://doi.org/10.1175/JCLI-D-12-00823.1

Semedo, A., Suvselj, K., Rutgersson, A., Sterl, A. (2011). A global view on the wind sea and swell climate and variability from ERA-40. Journal of Climate, 24(5), 1461-1479, https://doi.org/10.1175/2010JCLI3718.1

Seo, H., Subramanian, A. C., Miller, A. J., and Cavanaugh, N. R. (2014). Coupled impacts of the diurnal cycle of sea surface temperature on the Madden-Julian oscillation. Journal of Climate, 27(22), 8422-8443, https://doi.org/10.1175/JCLI-D-14-00141.1

Shelly, A., Xavier, P., Copsey, D., Johns, T., Rodriguez, J.M., Milton, S., and Klingaman, N. (2014). Coupled versus uncoupled hindcast simulations of the Madden-Julian Oscillation in the Year of Tropical Convection. Geophysical Research Letters, 41, 5670-5677, https://doi.org/10.1002/2013GL059062

Sluka, T., Penny, S.G., Kalnay, E. and Miyoshi, T. (2016). Assimilating atmospheric observations into the ocean using strongly coupled ensemble data assimilation. Geophysical Research Letters, 43(2), 752-759, https://doi.org/10.1002/2015GL067238

Smith, G. C., Bélanger, J. M., Roy, F., Pellerin, P., Ritchie, H., Onu, K., Roch, M., Zadra, A., Surcel Colan, D., Winter, B., Fontecilla, J.S., Deacu, D. (2018). Impact of coupling with an ice-ocean model on global medium-range NWP forecast skill. Monthly Weather Review, 146(4), 1157-1180, https://doi.org/10.1175/MWR-D-17-0157.1

Spreen, G., Kwok, R., Menemenlis, D., and Nguyen, A. T. (2017). Sea-ice deformation in a coupled ocean-sea-ice model and in satellite remote sensing data. The Cryosphere,11,1553-1573, https://doi.org/10.5194/tc-11-1553-2017

Staneva, J., Alari, V., Breivik, O., Bidlot, J.-R., Mogensen, K. (2017). Effects of wave-induced forcing on a circulation model of the North Sea. Ocean Dynamics, 67, 81-101, https://doi.org/10.1007/s10236-016-1009-0

Sutherland, G., and Rabault, J. (2016). Observations of wave dispersion and attenuation in landfast ice. Journal of Geophysical Research: Oceans, 121(3), 1984-1997, https://doi.org/10.1002/2015JC011446

Takano, K., Mintz, Y., Han, Y.-J. (1973). Numerical simulation of the world ocean circulation. Paper presented at the 2nd Conference on Numerical Prediction. Am. Meteorol. Soc. (1973), Monterey, CA (unpublished).

Uchiyama, Y., McWilliams, J. C., Shchepetkin, A. F. (2010). Wave-current interaction in an oceanic circulation model with a vortex-force formalism: Application to the surf zone. Ocean Modelling, 34(1), 16-35, https://doi.org/10.1016/j.ocemod.2010.04.002

Vannitsem, S., and Duan, W. (2020). On the use of near-neutral Backward Lyapunov Vectors to get reliable ensemble forecasts in coupled ocean–atmosphere systems. Climate Dynamics, 55, 1125-1139, https://doi.org/10.1007/s00382-020-05313-3

Vinayachandran, P. N., Davidson, F., and Chassignet, E. P. (2020). Toward Joint Assessments, Modern Capabilities, and New Links for Ocean Prediction Systems. Bulletin of the American Meteorological Society, 101(4), E485-E487, https://doi.org/10.1175/bams-d-19-0276.1

Wahle, K., Staneva, J., Koch, W., Fenoglio-Marc, L., Ho-Hagemann, H. T. M., and Stanev, E. V. (2017). An atmosphere-wave regional coupled model: Improving predictions of wave heights and surface winds in the southern North Sea. Ocean Science, 13(2), 289-301, https://doi.org/10.5194/os-13-289-2017

Wang, K., and Wang, C. (2009). Modeling linear kinematic features in pack ice. Journal of Geophysical Research: Oceans, 114(C12), https://doi.org/10.1029/2008JC005217

Williams, T.D., Bennetts, L.G., Squire, V.A., Dumont, D., Bertino, L. (2013). Wave-ice interactions in the marginal ice zone. Part 1: Theoretical foundations. Ocean Modelling, 71, 81-91, https://doi.org/10.1016/j.ocemod.2013.05.010

Wolf, J. (2008). Coupled wave and surge modelling and implications for coastal flooding. Advances in Geosciences, 17, 19-22, https://doi.org/10.5194/adgeo-17-19-2008

Wu, L.,Rutgersson,A.,Breivik,O.(2019).Ocean-wave-atmosphereinteractionprocesses inafully coupledmodelling system. Journal of Advances in Modeling Earth Systems,11, 3852 3874, https://doi.org/10.1029/2019MS001761

Wu, L., Staneva, J., Breivik,Ø., Rutgersson, A.,Nurser, A. J. G., Clementi, E., and Madec, G. (2019).Wave effects on coastal upwelling and water level. Ocean Modelling, 101405, https://doi.org/10.1016/J.OCEMOD.2019.101405

Zhang, S., Harrison, M. J., Rosati, A., and Wittenberg, A. T. (2007). System Design and Evaluation of Coupled Ensemble Data Assimilation for Global Oceanic Climate Studies. Monthly Weather Review, 135(10), https://doi.org/10.1175/MWR3466.1

Previous chapter 9