COORDINATORS
The main objective of an operational sea ice forecasting system is to provide users with a reliable estimate of the state of the ice cover and its temporal evolution. To meet this purpose, the system needs to be coupled to, or use data from, ocean and atmosphere forecasting systems. Some form of data assimilation is also required to counteract errors due to the chaotic nature of the atmosphere-ocean-ice system. Users of sea ice forecasting systems are either stakeholders operating in the Arctic or downstream service providers who use the information as an input to their own services. With a changing climate and a warming Arctic, the number of stakeholders interested in operating in that region is growing.
The Arctic is getting warmer with temperatures rising at approximately twice the rate of the global average (Overland et al., 2016) but also more attractive for business as its natural resources are becoming available for exploitation and transport for the first time in our history. These include about 13% of the world’s oil and gas resources as estimated by the United States Geological Survey (Gautier et al., 2009), gold and other metals, and 5.5% of the freshwater resources stored on Greenland (Kundzewicz et al., 2007). Changing environmental conditions are modifying ecosystems in diverse ways. In the Barents Sea, the cod are thriving thanks to warming conditions (Kjesbu et al., 2014). A migration behaviour of boreal generalist fishes to cooler waters is also observed in the Bering Sea (Mueter and Litzow, 2008). These changes have implications for fisheries management and more generally for the Arctic ecosystem. Cruise tourism in the Arctic is also developing fast since operators can offer comfortable icebreaker cruises all the way to the North Pole.
The NSR along the Russian coast of the Arctic, which was heavily used by the Soviet Union until the 1990’s, could again become an attractive alternative to reach East Asia from Western Europe. The route is indeed shorter than the one crossing Suez Passage (17000 km instead of 22000 km for a Rotterdam-Shanghai voyage) and would save fuel. However, in case of accidents, cargo and fuel would pose serious threats for the Arctic environment. Coastguards and navies of the Arctic nations must then be prepared for assisting vessels, performing search and rescue operations, and remediating oil spills in ice-infested waters, with frequently poor communication capabilities that may hinder access to new information.
The oil and gas exploration and production need sea ice forecasting both on local scales, to simulate individual ice floes on the theatre of their operations, and on large scales, to predict the time of the freeze up and break-up of the ice. It is expected that the exploration and production activities will be more active in relatively mild ice conditions than in severe ice conditions, which means that forecasts will have higher value for the MIZ than for the ice pack. The MIZ, defined as the ice-covered region under the influence of surface waves from the open ocean, is particularly in need of forecasts to prevent risks such as ice floe’s projections under the action of waves.

There are fewer stakeholder interests in the Southern Ocean, due to the reduced commercial activities in that region. However, ice-ocean predictions can provide information for tourism or scientific operations in the region, including access to Antarctic research stations and support for scientific research vessels. The complex rescue of a joint tourist-research vessel stuck within the Antarctic sea ice in December 2013 (A. Luck-Baker, BBC News, 21 January 2014, 🔗1 ), requiring assistance from two icebreakers and a helicopter, highlighted the need for reliable predictions even in such a remote region. On longer timescales, changing sea ice conditions have implications for ice-dependent wildlife in the region, such as emperor penguins (e.g., Jenouvrier et al., 2012), which raises associated wildlife management concerns.
The shipping industry is primarily concerned with very detailed ice concentration, thickness and compression (and marginally snow depths, because deep snow can also impede the progression of an icebreaker). On the other hand, in the aftermath of oil spills in ice-infested waters, search and rescue operations and forecasting are both dependent on ice motion and their diffusive properties that increase the search radius with time. The question of spatial and temporal resolution is especially critical for the latter case because of the strong scale-dependence of sea ice deformation rates (Rampal et al., 2008). In addition, the diffusion is higher in the chaotic MIZ than in the ice pack (Figure 6.1). The oil industry would ultimately need a detailed forecast of the position of each ice floe surrounding their operations for the day-to-day management of their activities, which can be only delivered by discrete-element models (Herman 2015, Rabatel et al., 2015). How to nest discrete-element models into the continuum sea ice models, considered in this chapter, remains an open question.
The physical processes simulated by sea ice models are commonly split into two: vertical processes, related to thermodynamic growth and melt, and mechanical and dynamical processes giving rise to horizontal movement of ice (Figure 6.2).
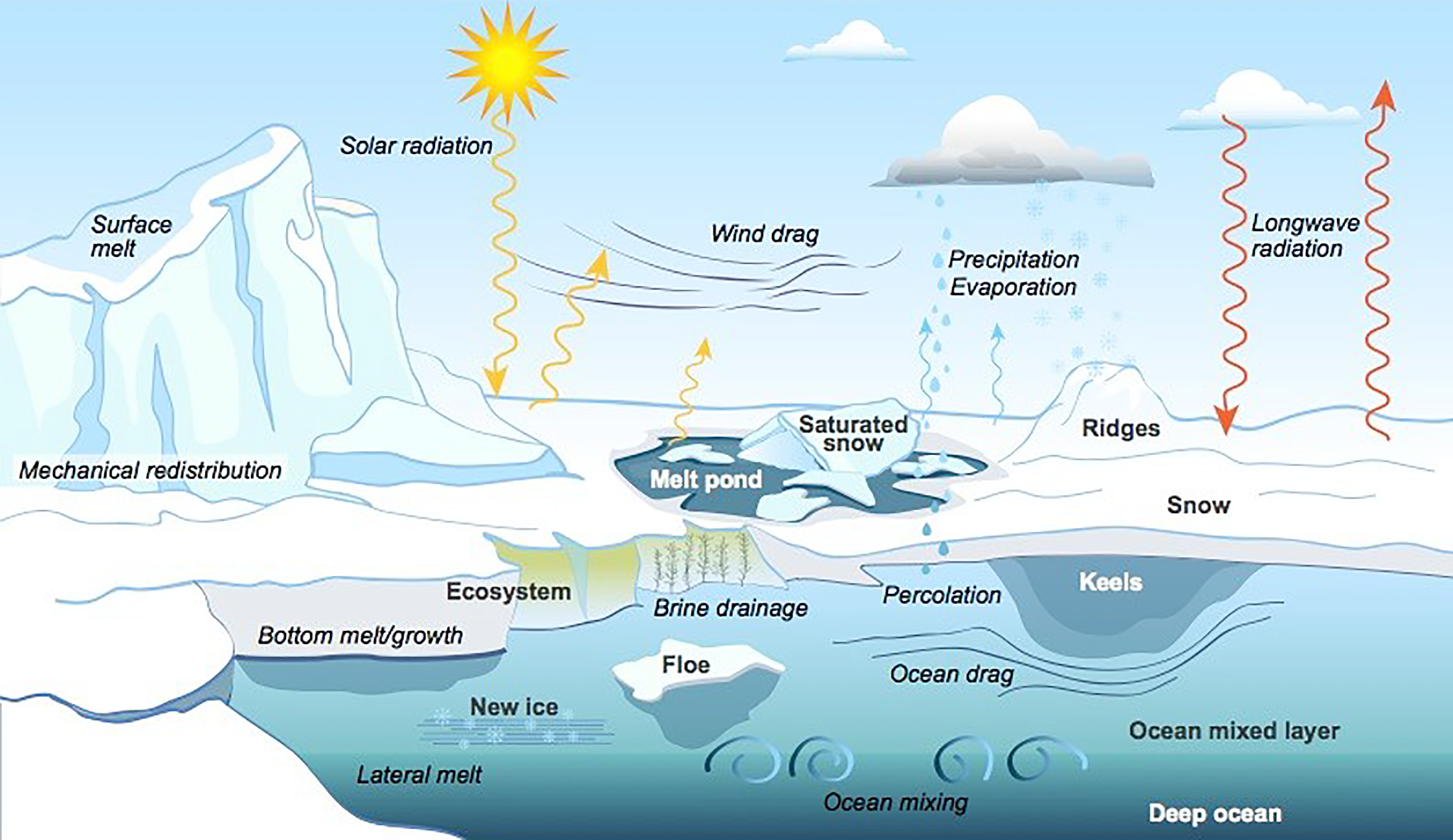
The thermodynamic growth and melt of ice can be thought of as the result of the diffusion of heat between ocean and atmosphere, through the ice. Additional complications arise primarily due to the presence of salt or brine pockets in the ice, and the presence of snow. The brine pockets affect the heat conductivity and heat capacity of the ice, while both heat conductivity and heat capacity of the snow, as well as its density, are affected by the state and type of snow, as well as snow metamorphosis.
The basics of thermodynamic modelling of sea ice have been well established since the early 70s (Maykut and Untersteiner, 1971), with the notable improvement in theoretical understanding brought by the application of mushy-layer theory to sea ice (Feltham et al., 2006), and substantial work relating to the dynamics of brine drainage and the multi-phase nature of sea ice (Vancoppenolle et al., 2007; Notz and Worster, 2009; Griewank and Notz, 2013). In terms of model development though, progress has been made in improving numerical performance and in technical aspects, such as conservation of heat, energy, and enthalpy (e.g., Semtner, 1976; Bitz and Libscomb, 1999; Winton, 2000; Huwald et al., 2005). Recently, the more advanced multiphase physics have also found its way into large-scale sea-ice models (Turner et al., 2013; Turner and Hunke, 2015).
The fundamentals of ice dynamics modelling are less firmly rooted in basic theoretical understanding. While most of the terms of the momentum equation are well understood and follow the basic formulation of the Navier-Stokes equation on a rotating sphere, the formulation of internal stresses is less certain. These describe the response of the ice to external forcing and are, as such, at the heart of sea ice dynamical modelling.
Sea ice is a solid material and, as such, can only move once fractured or broken. In most sea ice models this is taken into account by assuming a rate-independent (von Mises) plasticity. This approach was originally proposed by Coon et al. (1974) but reshaped into a more computationally tractable form in the viscous-plastic model proposed by Hibler (1979), in which the ice is assumed to deform in a linear-viscous manner until it reaches a plastic threshold, representing the fracturing or breaking of the ice. The fracturing process is, as such, simulated explicitly at the grid scale.
However, the process of ice fracturing has been shown to be the result of the propagation of fracturing events from small spatial scales to large ones (Weiss and Marsan, 2004). This results in fractal characteristics of the deformation rates (e.g., Marsan et al., 2004; Rampal et al., 2008; Stern and Lindsay, 2009¸ Schulson and Hibler, 2017). It means that a sea ice model hoping to correctly capture the deformation of the ice must account for this propagation of fracturing events from small to large scales. As the propagation starts at very small spatial and temporal scales (Oikkonen et al., 2017), a geophysical scale model must account for this through a sub-grid scale parameterisation.
The role and importance of fracture dynamics is still a hotly debated subject within the sea ice modelling community. The fractal nature of sea ice deformation is generally accepted and the scaling of deformation rates is recognised as a potential tool and metric for model evaluation and improvement (Rampal et al., 2016; Spreen et al., 2017; Hutter et al., 2018; Rampal et al., 2019; Bouchat et al., 2021). At the same time, it is still unresolved the question of whether to explicitly simulate the fracturing process at a very high resolution (Hutter et al., 2019) or to use a sub-grid scale parameterisation of the fracturing process at a more modest resolution (Dansereau et al., 2016; Rampal et al., 2016).
References

Adcroft, A., Anderson, W., Balaji, V., Blanton, C., Bushuk, M., Dufour, C. O., et al. (2019). The GFDL global ocean and sea ice model OM4.0: Model description and simulation features. Journal of Advances in Modelling Earth Systems, 11, 3167-3211, https://doi.org/10.1029/2019MS001726
Aydoǧdu, A., Carrassi, A., Guider, C.T., Jones, C. K. R. T., and Rampal, P. (2019). Data assimilation using adaptive, non-conservative, moving mesh models. Nonlinear Processes in Geophysics, 26(3), 175-193, https://doi.org/10.5194/npg-26-175-2019
Barth, A., Canter, M., Van Schaeybroeck, B., Vannitsem, S., Massonnet, F., Zunz, V., Mathiot, P., Alvera-Azcárate, A., Beckers, J.-M. (2015). Assimilation of sea surface temperature, ice concentration and ice drift in a model of the Southern Ocean. Ocean Modelling, 93, 22-39, https://doi.org/10.1016/j.ocemod.2015.07.011
Bertino, L., Bergh, J., and Xie, J. (2015). Evaluation of uncertainties by ensemble simulation, ART JIP Deliverable 3.3. NERSC, Bergen, Norway.
Bertino, L., Evensen, G., Wackernagel, H. (2003). Sequential Data Assimilation Techniques in Oceanography. International Statistical Review 71(2), 223-241, http://www.jstor.org/stable/1403885
Bitz, C. M. and Lipscomb, W. H. (1999). An energy-conserving thermodynamic model of sea ice. Journal of Geophysical Research: Oceans, 104(C7), 15669-15678, https://doi.org/10.1029/1999JC900100
Bitz, C. M., Holland, M. M., Weaver, A. J., and Eby, M. (2001). Simulating the ice-thickness distribution in a coupled climate model. Journal of Geophysical Research: Oceans, 106(C2), 2441-2463, https://doi.org/10.1029/1999JC000113
Blockley, E. W. and Peterson, K. A. (2018). Improving Met Office seasonal predictions of Arctic sea ice using assimilation of CryoSat-2 thickness. The Cryosphere, 12, 3419-3438, https://doi.org/10.5194/tc-12-3419-2018
Blockley, E., Vancoppenolle, M., Hunke, E., Bitz, C., Feltham, D., Lemieux, J., Losch, M., Maisonnave, E., Notz, D., Rampal, P., Tietsche, S., Tremblay, B., Turner, A., Massonnet, F., Ólason, E., Roberts, A., Aksenov, Y., Fichefet, T., Garric, G., Iovino, D., Madec, G., Rousset, C., Salas y Melia, D., Schroeder, D. (2020). The future of sea ice modeling: Where do we go from here? Bulletin of the American Meteorological Society, 101, E1302-E1309, https://doi.org/10.1175/BAMS-D-20-0073.1
Bouchat, A., Hutter, N.C., Chanut, J., Dupont, F., Dukhovskoy, D. S., Garric, G., Lee, Y. J., Lemieux, J.-F., Lique, C., Losch, M., Maslowski, W., Myers, P. G., Ólason, E., Rampal, P., Rasmussen, T.A.S., Talandier, C., Tremblay, B. (2021). Sea Ice Rheology Experiment (SIREx), Part I: Scaling and statistical properties of sea-ice deformation fields. Journal of Geophysical Research: Oceans,127(4), e2021JC017667, https://doi.org/10.1029/2021JC017667
Bouillon, S., Fichefet, T., Legat, V., and Madec, G. (2013). The elastic-viscous-plastic method revisited. Ocean Modelling, 71, 2-12, https://doi.org/10.1016/j.ocemod.2013.05.013
Bouillon, S., and Rampal, P. (2015). On producing sea ice deformation data sets from SAR-derived sea ice motion. The Cryosphere, 9, 663-673, https://doi.org/10.5194/tc-9-663-2015
Breivik, Ø. and Allen, A. A. (2008). An operational search and rescue model for the Norwegian Sea and the North Sea. Journal of Marine Systems, 69(1-2), 99-113, https://doi.org/10.1016/j.jmarsys.2007.02.010
Buizza, R., Houtekamer, P. L., Pellerin, G., Toth, Z., Zhu, Y., and Wei, M. (2005). A Comparison of the ECMWF, MSC, and NCEP Global Ensemble Prediction Systems. Monthly Weather Review, 133(5), 1076-1097, https://doi.org/10.1175/MWR2905.1
Castellani, G., Lüpkes, C., Gerdes, R., Hendricks, S. (2014). Variability of Arctic sea ice topography and its impact on the atmospheric surface drag. Journal of Geophysical Research: Ocean, 119(10), 6743-6762, https://doi.org/10.1002/2013JC009712
Cavalieri, D. J., Parkinson, C. L. (2012). Arctic Sea ice variability and trends, 1979-2010. The Cryosphere, 6,881-889, https://doi.org/10.5194/tc-6-881-2012
Cheng, S., Aydoğdu, A., Rampal, P., Carrassi, A., Bertino, L. (2020). Probabilistic Forecasts of Sea Ice Trajectories in the Arctic: Impact of Uncertainties in Surface Wind and Ice Cohesion. Oceans, 1(4), 326-342, https://doi.org/10.3390/oceans1040022
Chevallier, M., and Salas-Melia, D. (2012). The role of sea ice thickness distribution in the Arctic sea ice potential predictability: A diagnostic approach with a coupled GCM. Journal of Climate, 25(8), 3025-3038, https://doi.org/10.1175/JCLI-D-11-00209.1
Chevallier, M., Smith, G. C., Dupont, F., Lemieux, J.-F., Forget, G., Fujii, Y., et al. (2017). Intercomparison of the Arctic sea ice cover in global ocean-sea ice reanalyses from the ORA-IP project. Climate Dynamics, 49, 1107-1136, https://doi.org/10.1007/s00382-016-2985-y
Connolley, W. M., Gregory, J. M., Hunke, E., McLaren, A. J. (2004). On the Consistent Scaling of Terms in the Sea-Ice Dynamics Equation. Journal of Physical Oceanography, 34(7), 1776-1780, https://doi.org/10.1175/1520-0485(2004)034<1776:OTCSOT>2.0.CO;2
Coon, M. D., Maykut, G. A., Pritchard, R. S., Rothrock, D. A., Thorndike, A. S. (1974). Modeling the pack ice as an elastic-plastic material. AIDJEX Bulletin, 24, 1-106, Univ. of Wash., Seattle, 1974.
Coon, M., Kwok, R., Levy, G., Pruis, M., Schreyer, H., Sulsky, D. (2007). Arctic Ice Dynamics Joint Experiment (AIDJEX) assumptions revisited and found inadequate. Journal of Geophysical Research: Ocean, 112, C11S90, https://doi.org/10.1029/2005JC003393
Danilov, S., Wang, Q., Timmermann, R., Iakovlev, N., Sidorenko, D., Kimmritz, M., Jung, T., and Schröter, J. (2015). Finite-Element Sea Ice Model (FESIM), version 2. Geoscientific Model Development, 8, 1747-1761, https://doi.org/10.5194/gmd-8-1747-2015
Dansereau, V., Weiss, J., Saramito, P., and Lattes, P. (2016). A Maxwell elasto-brittle rheology for sea ice modelling. The Cryosphere, 10, 1339-1359, https://doi.org/10.5194/tc-10-1339-2016
Dobney, A., Klinkenberg, H., Souren, F., and Van Borm, W. (2000). Uncertainty calculations for amount of chemical substance measurements performed by means of isotope dilution mass spectrometry as part of the PERM project. Analytica chimica acta, 420, 89-94.
Dukhovskoy, D. S., Ubnoske, J., Blanchard-Wrigglesworth, E., Hiester, H. R., and Proshutinsky, A. (2015). Skill metrics for evaluation and comparison of sea ice models. Journal of Geophysical Research: Oceans, 120(9), 5910-5931. https://doi.org/10.1002/2015JC010989
Duraisamy, K. A., and Iaccarino, G. (2017). Assessing turbulence sensitivity using stochastic Monte Carlo analysis. Physical Review Fluids, https://arxiv.org/abs/1704.05187
Feltham, D. L., Untersteiner, N., Wettlaufer, J. S., and Worster, M. G. (2006). Sea ice is a mushy layer. Geophysical Research Letters, 33(14), L14501, ISSN 0094-8276, https://doi.org/10.1029/2006GL026290
Fenty, I., and Heimbach, P. (2013). Coupled sea ice–ocean state estimation in the Labrador Sea and Baffin Bay. Journal of Physical Oceanography, 43(5), 884-904, https://doi.org/10.1175/JPO-D-12-065.1
Fenty, I., Menemenlis, D., and Zhang, H. (2015). Global coupled sea ice-ocean state estimation. Climate Dynamics, 49, 931-956, https://doi.org/10.1007/s00382-015-2796-6
Flocco, D., Feltham, D., Turner, A. (2010). Incorporation of a physically based melt pond scheme into the sea ice component of a climate model. Journal of Geophysical Research: Oceans, 115, C08012, https://doi.org/10.1029/2009JC005568
Gautier, D. L., Bird, K. J., Charpentier, R. R., Grantz, A., Houseknecht, D. W., Klett, T. R., … Wandrey, C. J. (2009). Assessment of Undiscovered Oil and Gas in the Arctic. Science, 324, 1175-1179, https://doi.org/10.1126/science.1169467
Girard, L., Bouillon, S., Weiss, J., Amitrano, D., Fichefet, T., and Legat, V. (2011). A new modeling framework for sea-ice mechanics based on elasto-brittle rheology. Annals of Glaciology, 52, 123-132, doi:10.3189/172756411795931499
Girard-Ardhuin, F., and Ezraty, R. (2012). Enhanced Arctic Sea Ice Drift Estimation Merging Radiometer and Scatterometer Data. IEEE Transactions on Geoscience and Remote Sensing, 50(7), 2639-2648, doi:10.1109/TGRS.2012.2184124
Goessling H., Tietsche, S., Day, J.J., Hawkins, E., Jung, T. (2016). Predictability of the Arctic sea ice edge. Geophysical Research Letters, 43(4), 1642-1650, https://doi.org/10.1002/2015GL067232
Goessling, H. F., and Jung, T. (2018). A probabilistic verification score for contours: Methodology and application to Arctic ice-edge forecast. Quarterly Journal of the Royal Meteorological Society, 144, 735-743, https://doi.org/10.1002/qj.3242
Goessling, H. F. and the SIDFEx Team (2020). Making Use and Sense of 75,000 Forecasts of the Sea Ice Drift Forecast Experiment (SIDFEx), EGU General Assembly 2020, Online, 4-8 May 2020, EGU2020-18867, https://doi.org/10.5194/egusphere-egu2020-18867
Griewank, P. J., Notz, D. (2013). Insights into brine dynamics and sea ice desalination from a 1-D model study of gravity drainage. Journal of Geophysical Research: Oceans, 118, 3370-3386, doi:10.1002/jgrc.20247
Grumbine, R. W. (1998). Virtual Floe Ice Drift Forecast Model Intercomparison. Weather and Forecasting, 13, 886-890, https://doi.org/10.1175/1520-0434(1998)013<0886:VFIDFM>2.0.CO;2
Grumbine, R. W. (2013). Long Range Sea Ice Drift Model Verification. Camp. Springs, Maryland.
Guerreiro, K., Fleury, S., Zakharova, E., Rémy, F., and Kouraev, A. (2016). Potential for estimation of snow depth on Arctic sea ice from CryoSat-2 and SARAL/AltiKa missions. Remote Sensing of Environment, 186, 339-349, https://doi.org/10.1016/j.rse.2016.07.013
Gryanik, V. M., and Lüpkes, C. (2017). An Efficient Non-iterative Bulk Parametrization of Surface Fluxes for Stable Atmospheric Conditions Over Polar Sea-Ice. Boundary-Layer Meteorology, 166, 301-325, https://doi.org/10.1007/s10546-017-0302-x
Hackett, B., Breivik, Ø., Wettre, C. (2006). Forecasting the drift of objects and substances in the ocean. In E.P. Chassignet and J. Verron (ed.s) “Ocean Weather Forecasting, An Integrated View of Oceanography”, 507-524, Springer, Dordrecht.
Hebert, D. A., Allard, R. A., Metzger, E. J., Posey, P. G., Preller, R. H., Wallcraft, A. J., Phelps, M. W., and Smedstad, O. M. (2015). Short-term sea ice forecasting: An assessment of ice concentration and ice drift forecasts using the U.S. Navy's Arctic Cap Nowcast/Forecast System. Journal of Geophysical Research: Oceans, 120, 8327- 8345, https://doi.org/10.1002/2015JC011283
Herman, A. (2015). Discrete-Element bonded particle Sea Ice model DESIgn, version 1.3a - model description and implementation. Geoscientific Model Development, 9, 1219–1241, https://doi.org/10.5194/gmd-9-1219-2016
Hibler, W. D. (1979). A dynamic thermodynamic sea ice model. Journal of Physical Oceanography, 9, 817-846.
Hopkins, M. (2004). A discrete element Lagrangian sea ice model. Engineering Computations, 21, 409-421, https://doi.org/10.1108/02644400410519857
Hunke, E., and Dukowicz, J. (1997). An elastic-viscous-plastic model for sea ice dynamics. Journal of Physical Oceanography, 27(9), 1849-1867, https://doi.org/10.1175/1520-0485(1997)027<1849:AEVPMF>2.0.CO;2
Hunke, E., Hebert, D., Lecomte, O. (2013). Level-ice melt ponds in the Los Alamos sea ice model, CICE. Ocean Modelling, 71, 26-42, https://doi.org/10.1016/j.ocemod.2012.11.008
Hunke, E., Allard, R., Blain, P. et al. (2020). Should Sea-Ice Modeling Tools Designed for Climate Research Be Used for Short-Term Forecasting? Current Climate Change Reports, 6, 121-136, https://doi.org/10.1007/s40641-020-00162-y
Hunke, E., Allard, R., Bailey, D.A., Blain, P., Craig, A., Dupont, F., DuVivier, A., Grumbine, R., Hebert, D., Holland, M., Jeffery, N., Lemieux, J.F., Osinski, R., Rasmussen, T., Ribergaard, M., Roberts, A., Denise, W. (2021). CICE Version 6.3.0. http://doi.org/10.5281/zenodo.1205674
Hutter, N., Losch, M., and Menemenlis, D. (2018). Scaling properties of Arctic sea ice deformation in a high-resolution viscous-plastic sea ice model and in satellite observations. Journal of Geophysical Research: Oceans, 123, 672-687, https://doi.org/10.1002/2017JC013119
Hutter, N., Zampieri, L., Losch, M. (2019). Leads and ridges in Arctic sea ice from RGPS data and a new tracking algorithm. The Cryosphere, 13, 627-645, https://doi.org/10.5194/tc-13-627-2019
Huwald, H., Tremblay, L.-B., Blatter, H. (2005). A multilayer sigma-coordinate thermodynamic sea ice model: Validation against Surface Heat Budget of the Arctic Ocean (SHEBA)/Sea Ice Model Intercomparison Project Part 2 (SIMIP2) data. Journal of Geophysical Research: Oceans, 110, C05010, https://doi.org/10.1029/2004JC002328
Iovino, D., Masina, S., Storto, A., Cipollone, A., and Stepanov, V. N. (2016). A 1/16° eddying simulation of the global NEMO sea-ice–ocean system. Geoscientific Model Development, 9, 2665–2684, https://doi.org/10.5194/gmd-9-2665-2016
Ivanova, N., Johannessen, O. M., Pedersen, L. T., and Tonboe, R. T. (2014). Retrieval of Arctic Sea Ice Parameters by Satellite Passive Microwave Sensors: A Comparison of Eleven Sea Ice Concentration Algorithms, IEEE Transactions on Geoscience and Remote Sensing, 52, 7233-7246, doi:10.1109/TGRS.2014.2310136
Ivanova, N., Pedersen, L. T., and Tonboe, R. T. (2015). Inter-comparison and evaluation of sea ice algorithms: towards further identification of challenges and optimal approach using passive microwave observations. The Cryosphere, 9, 1797-1817, https://doi.org/10.5194/tc-9-1797-2015
Janjić, T., McLaughlin, D., Cohn, S. E., and Verlaan, M. (2014). Conservation of Mass and Preservation of Positivity with Ensemble-Type Kalman Filter Algorithms. Monthly Weather Review,142(2), 755-773, https://doi.org/10.1175/MWR-D-13-00056.1
Jenouvrier, S., Holland, M., Strœve, J., Barbraud, C., Weimerskirch, H., Serreze, M., Caswell, H. (2012). Effects of climate change on an emperor penguin population: analysis of coupled demographic and climate models. Available at https://core.ac.uk/download/pdf/9584173.pdf
Johnson, M., Proshutinsky, A., Aksenov, Y., Nguyen, A.T., Lindsay, R., Haas, C., Zhang, J., Diansky, N., Kwok, R., Maslowski, W., Häkkinen, S., Ashik, I., de Cuevas, B. (2012). Evaluation of Arctic sea ice thickness simulated by Arctic Ocean Model Intercomparison Project models. Journal of Geophysical Research: Oceans, 117(C8), https://doi.org/10.1029/2011JC007257
Kaminski, T., Kauker, F., Eicken, H., and Karcher, M. (2015). Exploring the utility of quantitative network design in evaluating Arctic sea ice thickness sampling strategies. The Cryosphere, 9, 1721 1733, https://doi.org/10.5194/tc-9-1721-2015
Kauker, F., Kaminski, T., Karcher, M., Giering, R., Gerdes, R., and Voßbeck, M. (2009). Adjoint analysis of the 2007 all time Arctic sea-ice minimum. Geophysical Research Letters, 36, L03707, doi:10.1029/2008GL036323
Kimmritz, M., Losch, M., Danilov, S. (2017). A comparison of viscous-plastic sea ice solvers with and without replacement pressure. Ocean Modelling, 115, 59-69, https://doi.org/10.1016/j.ocemod.2017.05.006
Kjesbu, O.S., Bogstad, B., Devine, J.A., Gjøsæter, H., Howell, D., Ingvaldsen, R.B., Nash, R.D. M., and Skjæraasen, J. E. (2014). Synergies between climate and management for Atlantic cod fisheries at high latitudes. Proceedings of the National Academy of Sciences of the United States of America,111(9), 3478-3483, https://doi.org/10.1073/pnas.1316342111
Korosov, A. A., and Rampal, P. (2017). A Combination of Feature Tracking and Pattern Matching with Optimal Parametrization for Sea Ice Drift Retrieval from SAR Data. Remote Sensing, 9(258), https://doi.org/10.3390/rs9030258
Kundzewicz, Z. W., Mata, L. J., Arnell, N. W., Doll, P., Kabat, P., Jimenez, B., Miller, K., Oki, T., Zekai, S. and Shiklomanov, I. (2007) Freshwater resources and their management. In: Parry, M. L., Canziani, O. F., Palutikof, J. P., van der Linden, P. J. and Hanson, C. E. (eds.) “Climate Change 2007: Impacts, Adaptation and Vulnerability. Contribution of Working Group II to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change”. Cambridge University Press, 173-210, ISBN 9780521880091
Kurtz, N., Farrell, S. L., Studinger, M., Galin, N., Harbeck, J. P., Lindsay, R., Onana, V. D., Panzer, B., and Sonntag, J. G. (2013). Sea ice thickness, freeboard, and snow depth products from Operation IceBridge airborne data. The Cryosphere, 7, 1035-1056, https://doi.org/10.5194/tc-7-1035-2013
Kwok, R. (2006). Contrasts in sea ice deformation and production in the Arctic seasonal and perennial ice zones. Journal of Geophysical Research: Oceans, 112(C2), https://doi.org/10.1029/2005JC003172
Kwok, R., Cunningham, G. F., Zwally, H. J., and Yi, D. (2007). Ice, Cloud, and land Elevation Satellite (ICESat) over Arctic sea ice: Retrieval of freeboard. Journal of Geophysical Research: Oceans, 112(C12), https://doi.org/10.1029/2006JC003978
Lauvernet, C., Brankart, J.-M. M., Castruccio, F., Broquet, G., Brasseur, P., and Verron, J. (2009). A truncated Gaussian filter for data assimilation with inequality constraints: Application to the hydrostatic stability condition in ocean models. Ocean Modelling, 27(1-2), 1-17. https://doi.org/https://doi.org/10.1016/j.ocemod.2008.10.007
Laxon S. W., Giles, K. A., Ridout, A. L., Wingham, D. J., Willatt, R., Cullen, R., Kwok, R., Schweiger, A., Zhang, J., Haas, C., Hendricks, S., Krishfield, R., Kurtz, N., Farrell S., and Davidson, M. (2013). CryoSat-2 estimates of Arctic sea ice thickness and volume. Geophysical Research Letters, 40, 732-737, https://doi.org/10.1002/grl.50193
Leith, C. E. (1974). Theoretical skill of Monte Carlo forecasts. Monthly Weather Review, 102(6), 409-418, https://doi.org/10.1175/1520-0493(1974)102<0409:TSOMCF>2.0.CO;2
Lemieux, J.-F., Tremblay, B., Sedlácek, J., Tupper, P., Thomas, S., Huard, D., and Auclair, J.-P. (2010). Improving the numerical convergence of viscous-plastic sea ice models with the Jacobianfree Newton Krylov method. Journal of Computational Physics, 229(8), 2840-2852, https://doi.org/10.1016/j.jcp.2009.12.011
Leutbecher, M., and Palmer, T. N. (2008). Ensemble forecasting. Journal of Computational Physics, 227(7), 3515-3539, https://doi.org/10.1016/j.jcp.2007.02.014
Lindsay, R. W., and Zhang, J. (2006). Assimilation of Ice Concentration in an Ice-Ocean Model. Journal of Atmospheric and Oceanic Technology, 23(5), 742-749, https://doi.org/10.1175/JTECH1871.1
Lindsay, R., Wensnahan, M., Schweiger, A., and Zhang, J. (2014). Evaluation of seven different atmospheric reanalysis products in the Arctic. Journal of Climate, 27(7), 2588-2606, https://doi.org/10.1175/JCLI-D-13-00014.1
Lisæter, K. A., Rosanova, J., Evensen, G. (2003). Assimilation of ice concentration in a coupled ice-ocean model, using the Ensemble Kalman filter. Ocean Dynamics, 53, 368-388, https://doi.org/10.1007/s10236-003-0049-4
Lisæter, K. A. (2009). A multi-category sea-ice model. Technical report 304. NERSC, Thormøhlensgt. 47, N-5006 Bergen, Norway.
Losch, M., D. Menemenlis, J.-M. Campin, P. Heimbach, and C. Hill, 2010. On the formulation of sea-ice models. Part 1: Effects of different solver implementations and parameterizations. Ocean Modelling, 33(1-2), 129-144, https://doi.org/10.1016/j.ocemod.2009.12.008
Lüpkes, C., Gryanik, V. M., Hartmann, J., Andreas, E. L. (2012). A parameterization, based on sea ice morphology, of the neutral atmospheric drag coefficients for weather prediction and climate models. Journal of Geophysical Research: Atmospheres, 117(D13), https://doi.org/10.1029/2012JD017630
Marsan, D., Stern, H., Lindsay, R., Weiss, J. (2004). Scale Dependence and Localization of the Deformation of Arctic Sea Ice. Physical Review Letter, 93(17), https://link.aps.org/doi/10.1103/PhysRevLett.93.178501
Maykut, G. A., and Untersteiner, N. (1971). Some results from a time-dependent thermodynamic model of sea ice. Journal of Geophysical Research (1896-1977), 76,1550-1575, https://doi.org/10.1029/JC076i006p01550
McPhee, M. G. (1975). Ice-ocean momentum transfer for the AIDJEX ice model. AIDJEX Bullettin, 29 , 93-111.
Melsom, A., Counillon, F., LaCasce, J. H., Bertino, L. (2012). Forecasting search areas using ensemble ocean circulation modeling. Ocean Dynamics, 62(8), 1245-1257, https://doi.org/10.1007/s10236-012-0561-5
Melsom, A., Palerme, C., Müller, M. (2019). Validation metrics for ice edge position forecasts. Ocean Science, 15(3), 615-630, https://doi.org/10.5194/os-15-615-2019
Mogensen, U. B., Ishwaran. H., Gerds, T. A. (2012). Evaluating Random Forests for Survival Analysis using Prediction Error Curves. Journal of Statistical Software, 50(11), 1-23, doi:10.18637/jss.v050.i11
Molteni, F., Buizza, R., Palmer, T. N., Petroliagis, T. (1996). The ECMWF Ensemble Prediction System: Methodology and validation. Quarterly Journal of the Royal Meteorological Society, 122, 73-119, https://doi.org/10.1002/qj.49712252905
Motra, H. B., Stutz, H., Wuttke, F. (2016). Quality assessment of soil bearing capacity factor models of shallow foundations. Soils and Foundations, 56(2), 265-276, https://doi.org/10.1016/j.sandf.2016.02.009
Mueter, F. J., Litzow, M. A. (2008). Sea ice retreat alters the biogeography of the Bering Sea continental shelf. Ecological Applications, 18(2), 309-20, https://doi.org/10.1890/07-0564.1
Notz, D., and Worster, M. G. (2009). Desalination processes of sea ice revisited. Journal of Geophysical Research: Oceans, 114(C5), https://doi.org/10.1029/2008JC004885
Notz, D., Jahn, A., Holland, M., Hunke, E., Massonnet, F., Stroeve, J., … Vancoppenolle, M. (2016). The CMIP6 Sea-Ice Model Intercomparison Project (SIMIP): Understanding sea ice through climate model simulations. Geoscientific Model Development, 9(9), 3427-3446, https://doi.org/10.5194/gmd-9-3427-2016
Oikkonen, A., Haapala, J., Lensu, M., Karvonen, J., Itkin P. (2017). Small-scale sea ice deformation during N-ICE2015: From compact pack ice to marginal ice zone. Journal of Geophysical Research: Oceans, 122(6), 5105-5120, https://doi.org/10.1002/2016JC012387
Ólason, E., Rampal, P., and Dansereau, V. (2021). On the statistical properties of sea-ice lead fraction and heat fluxes in the Arctic. The Cryosphere, 15, 1053-1064, https://doi.org/10.5194/tc-15-1053-2021
Ólason, E., Boutin, G., Korosov, A., Rampal, P., Williams, T., Kimmritz, M., Dansereau, V. (2022). A new brittle rheology and numerical framework for large-scale sea-ice models. Submitted to Journal of Modelling the Earth System (JAMES), https://doi.org/10.1002/essoar.10507977.2
Overland, J.E, Dethloff, K., Francis, J.A., Hall, R.J., Hanna, E., Kim, S.-J., Screen, J.A., Shepherd, T.G., Vihma, T. (2016). Nonlinear response of mid-latitude weather to the changing Arctic. Nature Climate Change, 6, 992-999, https://doi.org/10.1038/nclimate3121
Perovich, D. K., Richter-Menge, J. A., Jones, K. F., Light, B. (2008). Sunlight, water, and ice: Extreme Arctic sea ice melt during the summer of 2007. Geophysical Research Letters, 35(11), https://doi.org/10.1029/2008GL034007
Petty, A. A., Markus, T., Kurtz, N. (2017). Improving our understanding of Antarctic sea ice with NASA's Operation IceBridge and the upcoming ICESat-2 mission. US CLIVAR Variations, 15(3), doi:10.5065/D6833QQP
Posey, P. G., Metzger, E.J., Wallcraft, A.J., Hebert, D.A., Allard, R.A., Smedstad, O.M., Phelps, M.W., Fetterer, F. , Stewart, J.S., Meier, W.N., and Helfrich, S.R. (2015). Improving Arctic sea ice edge forecasts by assimilating high horizontal resolution sea ice concentration data into the US Navy’s ice forecast systems. The Cryosphere, 9, 1735-1745, https://doi.org/10.5194/tc-9-1735-2015
Rabatel, M., Labbé, S., and Weiss, J. (2015). Dynamics of an Assembly of Rigid Ice Floes. J. Journal of Geophysical Research: Oceans, 120(9), 5887-5909, https://doi.org/10.1002/2015JC010909
Rabatel, M., Rampal, P., Carrassi, A., Bertino, L., and Jones, C.K.R T. (2018). Impact of rheology on probabilistic forecasts of sea ice trajectories: Application for search and rescue operations in the Arctic. The Cryosphere, 12, 935-953, https://doi.org/10.5194/tc-12-935-2018
Rampal, P., Weiss, J., Marsan, D., Lindsay, R., and Stern, H. (2008). Scaling properties of sea ice deformation from buoy dispersion analysis. Journal of Geophysical Research: Oceans, 113(C3), C03002, https://doi.org/10.1029/2007JC004143
Rampal, P., Bouillon, S., Ólason, E., and Morlighem, M. (2016). NeXtSIM: A new Lagrangian sea ice model. The Cryosphere, 10, 1055-1073, https://doi.org/10.5194/tc-10-1055-2016
Rampal, P., Dansereau, V., Olason, E., Bouillon, S., Williams, T., Korosov, A., and Samaké, A. (2019). On the multi-fractal scaling properties of sea ice deformation. The Cryosphere, 13, 2457-2474, https://doi.org/10.5194/tc-13-2457-2019
Richter-Menge, J. A., Perovich, D. K., Elder, B. C., Claffey, K., Rigor, I., Ortmeyer, M. (2006). Ice mass-balance buoys: a tool for measuring and attributing changes in the thickness of the Arctic sea-ice cover. Annals of Glaciology, 44(1), 205-210, doi:10.3189/172756406781811727
Rippeth, T.P. et al. (2015). Tide-mediated warming of Arctic halocline by Atlantic heat fluxes over rough topography. Nature Geoscience, 8(3), 191-194, https://doi.org/10.1038/ngeo2350
Rousset, C., Vancoppenolle, M., Madec, G., Fichefet, T., Flavoni, S., Barthélemy, A., Benshila, R., Chanut, J., Levy, C., Masson, S., and Vivier, F. (2015). The Louvain-La-Neuve sea ice model LIM3.6: global and regional capabilities. Geoscientific Model Development, 8, 2991-3005, https://doi.org/10.5194/gmd-8-2991-2015
Rösel, A., Kaleschke, L., and Birnbaum, G. (2012). Melt ponds on Arctic sea ice determined from MODIS satellite data using an artificial neural network. The Cryosphere, 6, 431-446, https://doi.org/10.5194/tc-6-431-2012
Sakov, P., Counillon, F., Bertino, L., Lisæter, K. A., Oke, P., and Korablev, A. (2012). TOPAZ4: an ocean-sea ice data assimilation system for the North Atlantic and Arctic. Ocean Science, 8, 633-656, https://doi.org/10.5194/os-8-633-2012
Schreyer, H. L., Sulsky, D. L., Munday, L. B., Coon, M. D., Kwok, R. (2006). Elastic-decohesive constitutive model for sea ice. Journal of Geophysical Research: Oceans, 111(C11), https://doi.org/10.1029/2005JC003334
Schulson, E. M., Hibler, W. D. (2017). The fracture of ice on scales large and small: Arctic leads and wing cracks. Journal of Glaciology, 27(127), 319-322, https://doi.org/10.3189/S0022143000005748
Semtner, A. J. (1976). A Model for the Thermodynamic Growth of Sea Ice in Numerical Investigations of Climate. Journal of Physical Oceanography, 6(3), 379-389. https://doi.org/10.1175/1520-0485(1976)006<0379:AMFTTG>2.0.CO;2
Simon, E., Samuelsen, A., Bertino, L., and Dumont, D. (2012). Estimation of positive sum-to-one constrained zooplankton grazing preferences with the DEnKF: a twin experiment. Ocean Science, 8(4), 587-602, https://doi.org/10.5194/os-8-587-2012
Smith, G. C., Roy, F., Reszka, M., Surcel Colan, D., He, Z., Deacu, D., Belanger, J.-M., Skachko, S., Liu, Y., Dupont, F., Lemieux, J.-F., Beaudoin, C., Tranchant, B., Drévillon, M., Garric, G., Testut, C.-E., Lellouche, J.-M., Pellerin, P., Ritchie, H., Lu, Y., Davidson, F., Buehner, M., Caya, A. and Lajoie, M. (2016). Sea ice forecast verification in the Canadian Global Ice Ocean Prediction System. Quarterly Journal of the Royal Meteorological Society, 142(695), 659-671, https://doi.org/10.1002/qj.2555
Smith, G. C., Liu, Y., Benkiran, M., Chikhar, K., Surcel Colan, D., Gauthier, A.-A., Testut, C.-E., Dupont, F., Lei, J., Roy, F., Lemieux, J.-F., and Davidson, F. (2021). The Regional Ice Ocean Prediction System v2: a pan-Canadian ocean analysis system using an online tidal harmonic analysis. Geoscientific Model Development, 14, 1445-1467, https://doi.org/10.5194/gmd-14-1445-2021
Spreen, G., Kwok, R., Menemenlis, D., and Nguyen, A. T. (2017). Sea-ice deformation in a coupled ocean– sea-ice model and in satellite remote sensing data. The Cryosphere, 11, 1553-1573, https://doi.org/10.5194/tc-11-1553-2017
Stark, J. D., Ridley, J., Martin, M., and Hines, A. (2008), Sea ice concentration and motion assimilation in a sea ice-ocean model. Journal of Geophysical Research: Oceans, 113(C5), https://doi.org/10.1029/2007JC004224
Stern, H., Lindsay, R. (2009). Spatial scaling of Arctic sea ice deformation. Journal of Geophysical Research: Oceans, 114(C10), https://doi.org/10.1029/2009JC005380
Sumata, H., Lavergne, T., Girard-Ardhuin, F., Kimura, N., Tschudi, M. A., Kauker, F., Karcher, M., Gerdes, R. (2014). An intercomparison of Arctic ice drift products to deduce uncertainty estimates. Journal of Geophysical Research: Oceans, 119(8), 4887-4921, https://doi.org/10.1002/2013JC009724
Tandon, N. F., Kushner, P. J., Docquier, D., Wettstein, J. J., and Li, C. (2018). Reassessing sea ice drift and its relationship to long-term Arctic sea ice loss in coupled climate models. Journal of Geophysical Research: Oceans, 123, 4338-4359. https://doi.org/10.1029/2017JC013697
Thorndike, A. S., Rothrock, D. A., Maykut, G. A., Colony, R. (1975). The thickness distribution of sea ice. Journal of Geophysical Research: Oceans, 80(33), 4501-4513, https://doi.org/10.1029/JC080i033p04501
Thorndike, A. S., Colony, R. (1982). Sea ice motion in response to geostrophic winds. Journal of Geophysical Research: Oceans, 87(C8), 5845-5852, https://doi.org/10.1029/JC087iC08p05845
Tian-Kunze, X., Kaleschke, L., Maaß, N., Mäkynen, M., Serra, N., Drusch, M., and Krumpen, T. (2014). SMOS-derived thin sea ice thickness: algorithm baseline, product specifications and initial verification. The Cryosphere, 8, 997-1018, https://doi.org/10.5194/tc-8-997-2014
Tonani M., et al. (2015). Status and future of global and regional ocean prediction systems. Journal of Operational Oceanography, 8(sup2), s201-s220, http://doi.org/10.1080/1755876X.2015.1049892
Toyoda, T., Hirose, N., Urakawa, L. S., Tsujino, H., Nakano, H., Usui, N., Fujii, Y., Sakamoto, K., and Yamanaka, G. (2019). Effects of Inclusion of Adjoint Sea Ice Rheology on Backward Sensitivity Evolution Examined Using an Adjoint Ocean-Sea Ice Model. Monthly Weather Review, 147(6), 2145-2162, https://doi.org/10.1175/MWR-D-18-0198.1
Tremblay, L.-B., and Mysak, L. A. (1997). Modeling Sea Ice as a Granular Material, Including the Dilatancy Effect. Journal of Physical Oceanography, 27(11), 2342-2360. https://doi.org/10.1175/1520-0485(1997)027<2342:MSIAAG>2.0.CO;2
Tsamados, M., Feltham, D. L., and Wilchinsky, A. V. (2013). Impact of a new anisotropic rheology on simulations of Arctic sea ice. Journal of Geophysical Research: Oceans, 118, 91-107, https://doi.org/10.1029/2012JC007990
Tsamados, M., Feltham, D. L., Schroeder, D., Flocco, D., Farrell, S. L., Kurtz, N., Bacon, S. (2014). Impact of Variable Atmospheric and Oceanic Form Drag on Simulations of Arctic Sea Ice. Journal of Physical Oceanography, 44, 1329-1353, https://doi.org/10.1175/JPO-D-13-0215.1
Turner, A. K., and Hunke, E. C. (2015). Impacts of a mushy-layer thermodynamic approach in global seaice simulations using the CICE sea-ice model. Journal of Geophysical Research: Oceans, 120, 1253-1275, https://doi.org/10.1002/2014JC010358
Turner, A. K., Hunke, E. C., and Bitz, C. M. (2013). Two modes of sea-ice gravity drainage: A parameterization for large-scale modeling. Journal of Geophysical Research: Oceans, 118, 2279-2294, https://doi.org/10.1002/jgrc.20171
Turner, A. K., Peterson, K. J., and Bolintineanu, D. (2022). Geometric remapping of particle distributions in the Discrete Element Model for Sea Ice (DEMSI v0.0). Geoscientific Model Development, 15, 1953-1970, https://doi.org/10.5194/gmd-15-1953-2022
Urrego-Blanco, J. R., Urban, N. M., Hunke, E. C., Turner, A. K., and Jeffery, N. (2016). Uncertainty quantification and global sensitivity analysis of the Los Alamos sea ice model. Journal of Geophysical Research: Oceans, 121, 2709-2732, https://doi.org/10.1002/2015JC011558
Usui, N., Ishizaki, S., Fujii, Y., Tsujino, H., Yasuda, T., Kamachi, M. (2006). Meteorological Research Institute multivariate ocean variational estimate (MOVE) system: Some early results. Advances in Space Research, 37/4), 806-822, https://doi.org/10.1016/j.asr.2005.09.022
Vancoppenolle, M., Bitz, C. M., and Fichefet, T. (2007). Summer landfast sea ice desalination at Point Barrow, Alaska: Modeling and observations. Journal of Geophysical Research: Oceans, 112(C4), https://doi.org/10.1029/2006JC003493
Vancoppenolle, M., Fichefet, T., Goosse, H., Bouillon, S., Madec, G., and Maqueda, M. A. M. (2009). Simulating the mass balance and salinity of Arctic and Antarctic sea ice. 1. Model description and validation. Ocean Modelling, 27(1-2), 33-53, https://doi.org/10.1016/j.ocemod.2008.10.005
Wackernagel, H. (2003). Multivariate Geostatistics. An Introduction with Applications. Springer Science & Business Media, 12 feb 2003 - 388 pp.
Waters, J., Lea, D.J., Martin, M.J., Mirouze, I., Weaver, A., and While, J. (2015). Implementing a variational data assimilation system in an operational 1/4 degree global ocean model. Quarterly Journal of the Royal Meteorological Society, 141(687), 333-349, https://doi.org/10.1002/qj.2388
Weiss, J., and Marsan, D. (2004). Scale properties of sea ice deformation and fracturing. Comptes Rendus Physique, 5(7), 735-751, https://doi.org/10.1016/j.crhy.2004.09.005
Wilchinsky, A. V., and Feltham, D. L. (2004). A continuum anisotropic model of sea-ice dynamics. Proceedings of the Royal Society A, 460(2047), https://doi.org/10.1098/rspa.2004.1282
Williams, T., Korosov, A., Rampal, P., Ólason, E. (2021). Presentation and evaluation of the Arctic sea ice forecasting system neXtSIM-F. The Cryosphere, 15, 3207-3227, https://doi.org/10.5194/tc-15-3207-2021
Winton A. (2000). A Reformulated Three-Layer Sea Ice Model. Journal of Atmospheric and Oceanic Technology, 17(4), 525-531, https://doi.org/10.1175/1520-0426(2000)017%3C0525:ARTLSI%3E2.0.CO;2
WMO (1970). Sea-ice nomenclature, terminology, codes and illustrated glossary. WMO Rep. WMO/OMM/ BMO 259, 121 pp.
Xie, J., Bertino, L., Counillon, F., Lisæter, K. A., and Sakov, P. (2017). Quality assessment of the TOPAZ4 reanalysis in the Arctic over the period 1991–2013. Ocean Science, 13(1), 123-144, http://doi.org/10.5194/os-13-123-2017
Zygmuntowska, M., Rampal, P, Ivanova, N., and Smedsrud, L. H. (2014). Uncertainties in Arctic sea ice thickness and volume: new estimates and implications for trends. The Cryosphere, 8, 705-720, https://doi.org/10.5194/tc-8-705-2014
To start contributing, sharing knowledge and editing the WIKI, please login !

Follow us