Wave modelling

Waves are extremely important in OOFS. This section gives an overview of the main challenges foreseen by OOFS for predictions to be able to numerically represent some relevant processes like that in Figure 8.1.

Why is a comprehensive and reliable wave forecast so important?

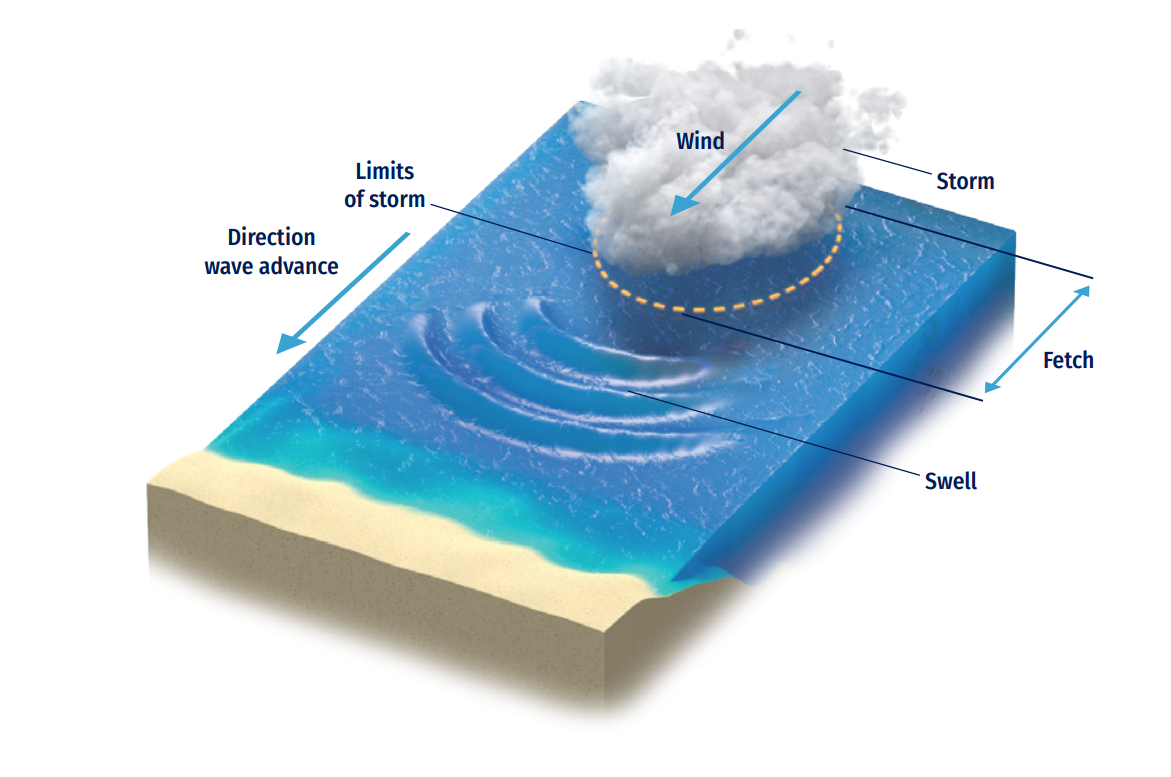
In the last decade, the worldwide seas were hit by severe storms (see ECMWF, 2020), which caused serious damages in offshore and coastal zones, and attracted public attention on the importance of having reliable and comprehensive wave forecasts, especially when extreme events occur (Figure 8.2). Additionally, human activities, such as offshore wind power industry, oil industry, and coastal recreation also necessitate regular operational sea state information with high resolution in space and time.

Furthermore, extreme waves can cause serious impacts over coastal environments and infrastructures. The design of coastal and offshore structures requires a reliable estimation of maximum wave height. Efforts of sea state information are directed towards the improvement of environmental loads definition for lifetime of a ship or structure (e.g. wind energy turbines or oil and gas platforms). For example, long-term statistical and high-resolution predictions of significant wave height are necessary for planning the maintenance operations of offshore wind farms. Subject to wave forecasts, in the days and hours preceding a mission, “go/no go” decisions are made on operations and maintenance activities in offshore wind farms. Indeed, a reduction of uncertainties on metocean conditions will have a direct impact on structure and mooring loads, both for ultimate limit state and fatigue design, as well as for warning criteria for ships. These results can be obtained through hindcast and forecast studies including maximum wave parameters, which also aim at expanding the wave Copernicus Marine Service products catalogue 🔗1 by providing novel wave diagnostics.

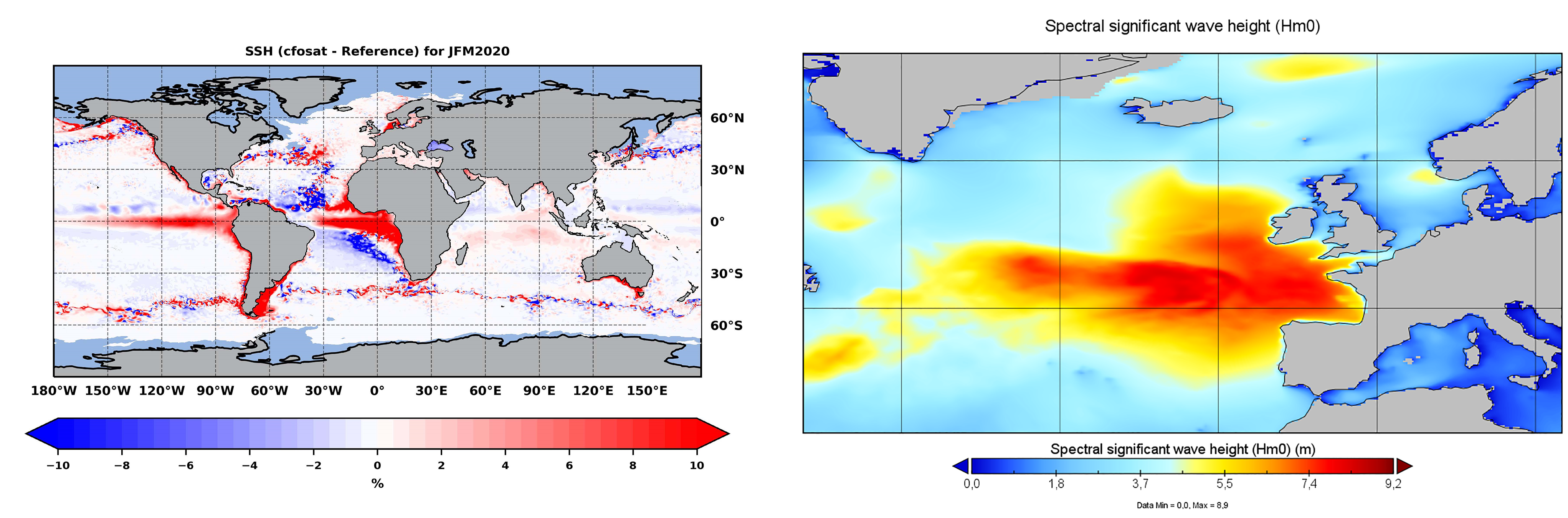
The level of performance of wave forecasting products is of crucial importance. The assimilation of novel satellite data in global Monitoring and Forecasting Centres has pointed out the skill of the systems during storms generating high waves (Aouf, 2018). The joined satellite and model analyses also demonstrate the capability of the wave forecasting products to cover from global to regional scales (Copernicus Marine Service, OSR 🔗2), as well as the potential benefits of merging observational and modelled products (such as those shown in Figure 8.3) provided by the Copernicus Marine Service.

Monitoring and forecasting

Monitoring and forecasting of wind waves are, in most cases, closely linked with ocean and atmospheric observations and modelling. The availability of systematic near-real time ocean observations is a prerequisite for the quality of weather and ocean state forecasts. Novel satellite wave observations are crucial for reducing the uncertainties in prediction skills for the wave simulations. Given that most of the buoy observations are coastal, remote sensing data are needed for tuning and validating the models offshore. On the other hand, ocean waves have a clear signature in most ocean remote sensing techniques, either adding noise or biases, and stable corrections and detection are very important for sea level and velocity estimates from altimetry (Climate Change Initiative Coastal Sea Level Team, 2020; Marti et al., 2021). It is important to underline that future regular monitoring of maximum wave heights is expected to improve understanding of the conditions that favour the generation of very large waves in the global ocean.

Sea state information for applications

There is a steady growth of the already intense interest in the wave conditions in coastal areas at different time scales. Increasing maritime traffic, recreational activities, urban development, ecosystem restoration, renewable energy industry, offshore management, all push in this direction (Cavaleri et al., 2018). Indeed, sea state affects most of the activities at sea (shipping, oil and gas industry, fisheries, offshore aquaculture, etc.), on the coast (marine protected areas, harbours, marine renewable energy, tourism, etc.). These activities require precise information on the sea state (hindcast, nowcast and forecast) and, in particular, on wave extremes. In addition to activities directly linked to the ocean, wind waves are of general interest to the Earth system.

Extreme events

Wind waves constitute the most relevant ocean process affecting the human activities and nearshore environment. The sea state and its related spatio-temporal variability dramatically affect maritime activities and the physical connectivity between offshore waters and coastal ecosystems, impacting also on the biodiversity of marine protected areas (Hewitt, 2003; González-Marco et al., 2008). Given their destructive effects in both the shoreline environment and human infrastructures, significant efforts have been devoted to predict extreme wave height events, prompting a wide range of adaptation strategies to deal with natural hazards in coastal areas (Hansom et al., 2015). In addition, there is also the emerging question about the effects of anthropogenic global climate change on present and future sea state conditions.

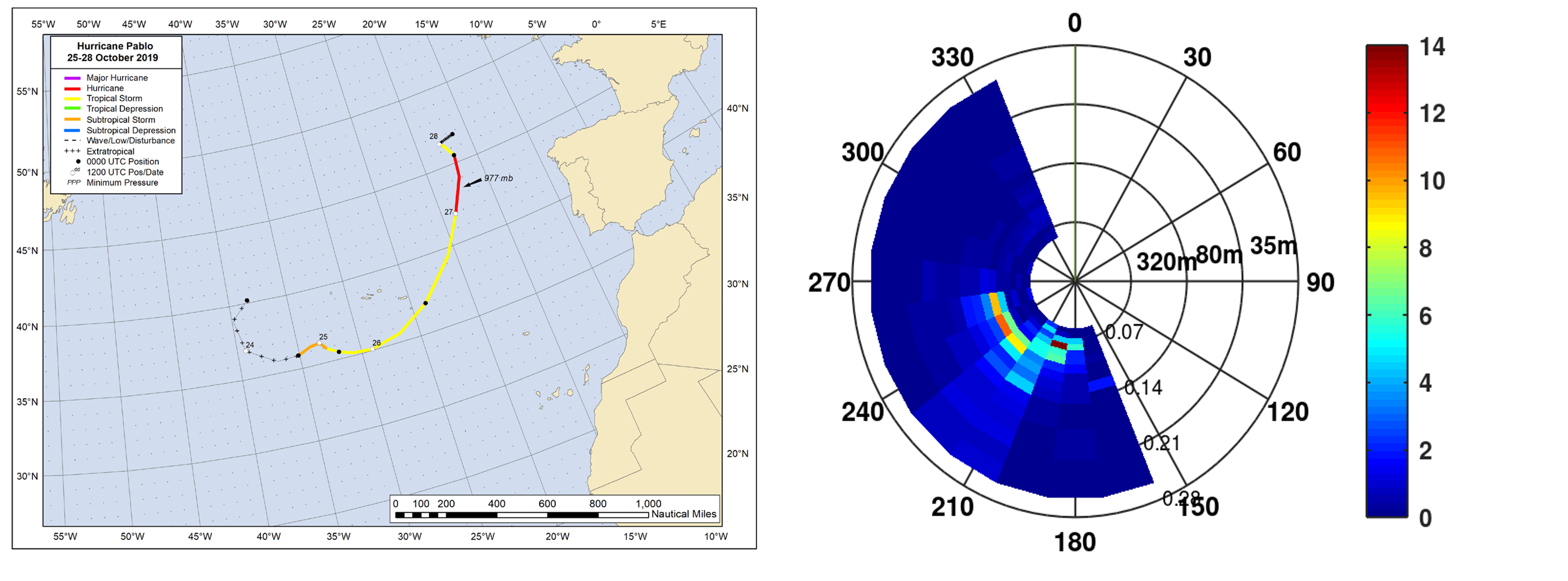
Tropical cyclones are commonly linked to devastation by hurricane force winds, storm surges and strong rainfall. They are also responsible for large exchanges of heat in the upper ocean and the atmosphere, and the transport of water from ocean to land. However, the dynamics inside these extremes are poorly sampled and understood. SAR overcomes these situations, but it is only able to recover one-dimensional information, which limits the ac<Zcuracy of estimated quantities like wind speed, total surface current, and wave spectra. In tropical cyclones, wave spectra (e.g. from Sentinel or by the CFOSAT) can only partly be recovered, as the quickly changing sea surface limits the resolution of SAR in the azimuth direction (Ardhuin et al., 2020) and from SWIM instrument of CFOSAT mission (Figure 8.4). 

Coupling with circulation 

The combined effect of high waves and sea level surge aggravate the storm risk potential. Integration of local wave and sea level forecasting systems (Álvarez-Fanjul et al., 2018; Staneva et al., 2020) and their associated alerts demonstrated the urgent need for such services. In respect to deep open waters, the relevance of currents is a difference emerging often. In the past, especially in the deep ocean, surface currents did not reach velocities to substantially affect wave conditions, which led to ignoring the wave induced currents in the ocean forecasts. However, close to the coast, the currents (barotropic and baroclinic) are geographically enhanced reaching values that, if not considered, can lead to substantial errors in wave model results (Cavaleri et al., 2018). Coupling between wind waves and circulation model waves can also affect the predictions of water levels, and thus of storm surges through changes in the stress of the upper-ocean mixing and circulation (Thomas et al., 2008; Staneva et al., 2021), providing more accurate offshore wave spectra (Cavaleri et al., 2018). Besides, forecasting the Lagrangian behaviour of surface currents is a key to identify high-risk scenarios for pollution of coastal areas, search and rescue, marine plastic, or quantify transport and retention of larvae or other planktonic organisms, with impact for fishery and Marine Protected Areas management.

Mixing

Human activities that take place at the atmospheric and ocean mixed layer (e.g. offshore wind energy sector) are largely driven by the air-sea exchanges of momentum, heat, and gas transfer. The fluxes between atmosphere and ocean are usually parameterized using bulk formulations, in which coefficients are often a function of wind speed alone. For example, ocean waves largely define air-sea fluxes and upper ocean mixing (Babanin et al., 2012; Veron, 2015). A considerably enhanced momentum transfer from the atmosphere to the wave field is found during growing sea state (young sea) (Janssen, 1989). A wind stress formulation depending on wind stress and the wind–wave momentum released to the ocean was proposed by Janssen (1991). When running stand-alone ocean or atmosphere models, the surface waves that represent the air-sea interface are not taken into account. This can cause biases about the upper ocean, due to insufficient or, in some cases, too strong mixing (Breivik et al., 2015), or even because the momentum transfer is shifted in time and space compared to how the fluxes would behave in the presence of waves. Recent analyses show a moderate impact for intermediate wind speeds (Edson et al., 2013), even though it is expected that the surface roughness caused by waves should play a role (Donelan, 2004), although it is often correlated with the wind speed. The impact of waves on upper ocean mixing and sea surface temperature, in particular in cases of shallow mixed layers, is clearer at global and regional scales (Janssen, 2012; Staneva et al., 2017; Law Chune et al., 2018); see an example in Figure 8.5.

Engineering and near coastal applications

In order to design and operate ocean and coastal infrastructures (e.g. dikes, harbours, etc.) wave climate data and wave statistics are crucial. High-resolution, high-skill wave forecasts are important for coastal and marine engineering, given that waves can damage marine infrastructures and affect the safety of shipping, ports, and offshore operations. Waves contribute to a large extent to shoreline erosion and flooding, which can influence coastal ecosystems and affect coastal communities. Realistic assessment and good understanding of historical wave climate is important to successfully address challenges and opportunities caused by present and future climate change, such as reduction of sediment supply by rivers to sand mining, blocking of longshore sediment transport by ports and other structures, sea level rise, particularly near tidal inlets, and land subsidence. Wind waves force coastal bathymetry changes and in coastline evolution, especially during extreme events orlarge swell events, waves can damage beaches, dunes, and/or dikes.

Early warning systems and risks

Warnings from integrated high-resolution wind waves surge forecasting systems can be sent in advance to the users. Several actions can be carried out to mitigate the impact of extreme hydrometeorological events. For example, harbours would stop operations to prevent accidents and assure safety. In some events material damages can be considerable but, as a result of preventive actions, personal injury can be avoided. Thanks to freely available satellite imagery (e.g. Sentinel), it is now possible to observe from nadir altimeters, with good accuracy and increased sampling, the coastline changes by significant wave height, as shown in Figure 8.6.

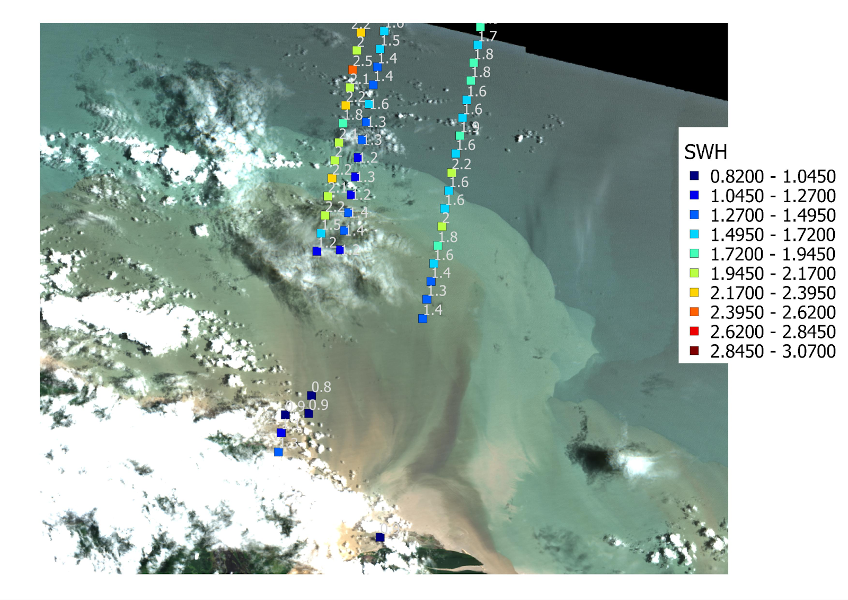
The assimilation of newly available satellite-based wave data in wind wave models allows to more accurately hindcast and forecast coastal evolution in remote and ungauged areas, and to assess the effectiveness of coastal management strategies. Wind wave forecasts directly may improve the safety of people working offshore, such as those on oil platforms, fishers, etc. Professional sailors are constantly looking for wave forecast products that improve their knowledge and forecasts of sea state to be able to make the best decisions about routes and actions they will take during month-long competitions.

Sea state and coastal ecosystems

Some coastal ecosystems, such as salt marshes, coral reefs, mangroves, and seagrass meadows, play a fundamental role in shaping nearshore processes in a large portion of the world's coastline. Due to their capacity to naturally mitigate coastal flooding and erosion, the management and protection of these ecosystems is increasingly advocated within nature-based coastal protection initiatives. Awareness that Nature-based solutions (NBS) can tackle societal challenges by utilising environmentally safe operations for vulnerability and risk assessment processes is growing. For example, marine seagrass is highly considered as a useful NBS, as it is capable of attenuating the impact of storm surges and coastal erosion. Ecosystem models usually have significant uncertainty in predictions. Understanding and better predicting wave-driven nearshore processes would help to improve our knowledge of hydrodynamic interactions with ecosystems across different time and space. Furthermore, wave forecast data are needed for activities involving protection, development, and enhancement of coastal and marine environments. Besides, sea state information can provide technical and scientific support to policy makers and stakeholders for environmental governance.

Wave data and the industry (e.g. marine energy sector, shipping operations, emergency response, etc.)

Wave data are critical for safe and efficient design, installation and operation of assets of the marine energy sector. High-resolution regional and coastal wave models can help to improve downscaling of general sea state forecasts, identify hotspots of different wave height properties, and prioritisation of maintenance jobs in offshore wind turbines, reducing their maintenance cost. Applications can further include initial resource assessment (wave power), environmental assessment, and planning (e.g. for installation and execution, operation and maintenance).

Sea state conditions have a significant impact on the design and structure of how vessels are built. The changes of the sea state impact on vessels operations and have always been a challenge for seafarers to which they have had to continually adapt. Besides, shipping/cargo operations are highly impacted by sea state and weather conditions. In addition, wave forecasts are needed for oil spill and emergency responses. The industry has developed various ways to adapt to the strength of the ocean. As evolving design and commercial needs push the boundaries of vessels‘ size and capacity, the demand for accurate sea state information increases.

Climate and waves as a part of the Earth system models

In our “blue” planet, interactions between the atmosphere and the ocean are crucial for the climate, and sea-related research plays a key role for a sustainable future (Visbeck, 2018), as advocated by international initiatives like the United Nations Decade of Ocean Science for Sustainable Development (2021-2030). Recent studies (e.g., Hewitt et al., 2017) have shown the relevance of air-sea interaction for a wide variety of phenomena (e.g. tropical/extratropical cyclogenesis, storm tracks, and global energy/radiation balances). Moreover, the IPCC has recognized the relevance of ocean waves for natural hazards in coastal areas, pointing out the need for more mature regional (coupled) downscaling. Furthermore, air-sea transfers will become even more critical in the future, due to enhanced interface transients, temperature gradients, and possible other factors. To address the uncertainty and sensitivity of future projections due to global warming, it is necessary to fill the knowledge gaps related to air-sea feedbacks, which also limit present weather modelling, advancing from semi-empirical (bulk) formulations to sea-state dependent equations with an enhanced process basis. There is also an urgent need to advance the understanding and improve the modelling capabilities of the air-sea boundary, in which wind-waves play a key role.

The atmosphere-ocean feedback has now become state-of-the-art in weather prediction, but their bearing in climate simulations is somewhat limited and warrants a more detailed assessment (Breivik et al., 2015). The modulation of the active air-sea interface alters atmospheric and oceanic dynamics, as well as the associated bio-geo-chemical fluxes (e.g. CO2 fluxes and storage at sea). Sea-state coupling should be accounted for in predictions/projections, so that the wave modulating effect on weather and climate evolution can be properly reproduced (Parkinson and Cavalieri 2012). Within an appropriate coupling and downscaling/nesting strategy, gaining understanding of air-sea interactions would reduce uncertainty in forecasting and be a critical advance for climate projections. Air-sea interface may have a role well beyond that conventionally accepted, and non-linear feedback should become more crucial under changing climate.

It is then essential to introduce the role of sea-state in both global and regional models for climate projection, addressing the resulting implications for bio geochemical and boundary (sea-ice and land) processes. Enhanced ESMs can be supported by new satellites (e.g. CFOSAT, Sentinel data, etc.) to achieve improved predictions for energetic conditions (e.g. tropical cyclones or Mediterranean tropical-like cyclones, often referred to as medicanes) and projections. In an ESM, the sea state needs to be considered at both global and regional scales, ensuring consistency and contributing to overcome uncertainties of projections at both short-term and long-term time scales. The advances on air-sea-wave-ice interactions in coupled models (including the land boundary) will contribute to bridge the gap between predictions/projections.

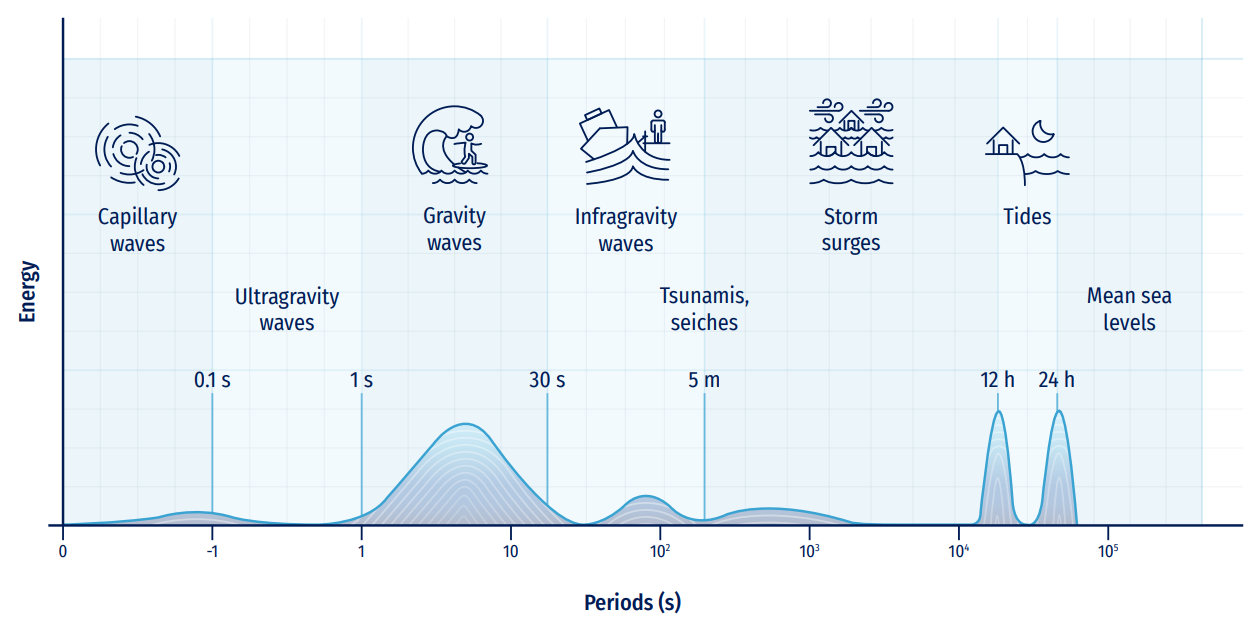
Within the catalogue of physical meteo-oceanographic variables and processes offered by any OOFS, waves can be considered one of the most relevant elements. Waves have high interaction with human activities located on the coast (coasts, ports, river mouths, etc.) given their energetic importance, and their cyclical and continuous presence in nature. Figure 8.7 displays the energetic relevance of wind-generated waves (with typical periods between 1 and 30s), in comparison with other oscillatory variables in the marine physical environment.

Traditionally, observations of ocean waves were obtained through visual databases (Gulev et al., 2003) limited in space and time, and with a high uncertainty about their qualitative genesis. Likewise, instrumental wave databases (Chelton and McCabe, 1985), obtained at discrete points in ocean and coastal areas, have been relevant in the understanding, quantification, and exploitation of this variable. However, only records of no more than two decades duration, generally non-continuous and acquired by equipment with non-homogeneous hardware characteristics, were available.

More recently, thanks to satellite technology it is possible to rely on a more extensive, continuous, accurate and homogeneous wave database (Barstow et al., 2004; Ribal and Young, 2019), with approximately two decades of development in the state of the art. The major disadvantage of this type of data consists in the spatial discontinuity conditioned by the satellite’s own translation, which only manages to cover narrow trajectories (see Chapter 4, Section 4.2.3).

In the same way, thanks to technological advances in computers, in recent years it has been possible to obtain continuous, homogeneous, and realistic wave databases with global coverage (Saha et al., 2010; Reguero et al., 2012; Perez et al., 2017), in line with directional calibration techniques for post-processing this type of series. These new databases are in turn fed by global climate models of wind, pressure, ice cover, and other variables (Tolman, 2010). See in Figure 8.8 a general scheme of variables and processes for wind-generated waves.

The wave variable represents one of the fundamental bases of meteo-oceanographic knowledge, due to its energy and interactions with natural and human activities in open and coastal areas. Therefore, it is important to have a good quantification of wave characteristics, either from a statistical (long-term or multi-year / hindcast databases) or predictive (short- to medium-term / forecast strategies) approach. This information is needed to design, construct, and operate maritime activities from coastal areas to offshore locations exposed to extreme events, as well as for environmental management, climate analysis, and all situations in which the complex processes of wave transformation occur.

The current techniques require long-time (historical) series on the most relevant wave variables, associated to sea states (generally hourly) with a global coverage. These databases are already available, often free of charge, thanks to important technological efforts of different institutions worldwide (Rascle et al., 2008; National Centers for Environmental Prediction, 2012; Le Traon et al., 2019). This reliable information is subjected to validation, assimilation, and calibration protocols with instrumental data (Thomas, et al., 2008; Stopa, 2018) but, as it is only limited to open water areas, does not usually include the transformation processes that waves undergo in intermediate to reduced waters. Then, to include these relevant processes, it is necessary to address the concept of wave downscaling, and additional physics is needed to characterise in detail and with high resolution the waves in coastal areas, harbours, beaches, etc.

Modern downscaling relies almost entirely on the support of numerical models that, over the last decade, have evolved enormously in terms of resolution, including physical processes, spatial extensions; also the variables to be obtained go beyond the basic wave variables. However, the new processes/variables to be obtained, along with the new numerical tools, tend to increase the complexity of the solutions, since they call upon for increasingly sophisticated mathematical formulations, rise the dimensions of the computational scheme (from two-dimensional to three-dimensional scopes) and, consequently, boost the computational time for their solution.

This trend represents an important technical constraint in the assembly of numerical solutions for obtaining the wave variables, from hourly to multi-annual statistical analysis, as well as for any analytical project in the predictive or forecast environment, in which the results are expected to be available on a daily basis and within a calculation window of a few minutes/hours.

Different methods have been proposed in the literature (Gaslikova and Weisse, 2005; Camus, et al. 2011 and Camus, et al. 2013) to overcome this problem, with the purpose of a better understanding of the complexity of the physical processes associated with the generation / propagation of waves, without paying a computational cost that moves the climate solution away from its practical and efficient objective.

In this chapter are discussed the most relevant concepts on the quantification of the wave variable in the meteo-oceanographic field, focusing on how to obtain time series (hourly) of this variable in the multi-annual field (hindcast) and the predictive field that are part of an OOFS. Basic concepts are:

• Theoretical definition of waves;
• Techniques, tools, and numerical models that are currently commonly used worldwide;
• Architecture and singularities in the solution schemes, assembly, and general approximation methods for the adequate exploitation of the tools;
• Basic and advanced variables associated with waves that can be obtained in different geographical areas;
• Some examples of multi-annual and forecast systems currently operating at the global level.

In line with the ten challenges of the UN Decade of Ocean Science for Sustainable Development, this chapter aims at making the readers able to obtain general and basic knowledge of wave climate, enabling them to establish their own multi-annual statistical prediction and interpretation systems for studies and projects in coastal engineering, offshore maritime works, beach design, integrated coastal management, harbour agitation, forensic analysis of extreme events, design formulations for coastal engineering, marine construction aid systems, etc.

This section describes the general terminology for the physical features of the ocean waves. Theoretical water waves are described by their length (L), height (H), amplitude (a) or height (H), and water propagation depth (d). Other variables, such as velocities, pressures and accelerations can be explicitly mathematically calculated from the three basic quantities: amplitude (a), wavelength (L) and period (T). Two-dimensional wave schematic is traditionally visualised (Dean and Dalrymple, 1991) to better understand the wave main characteristics (Figure 8.9).

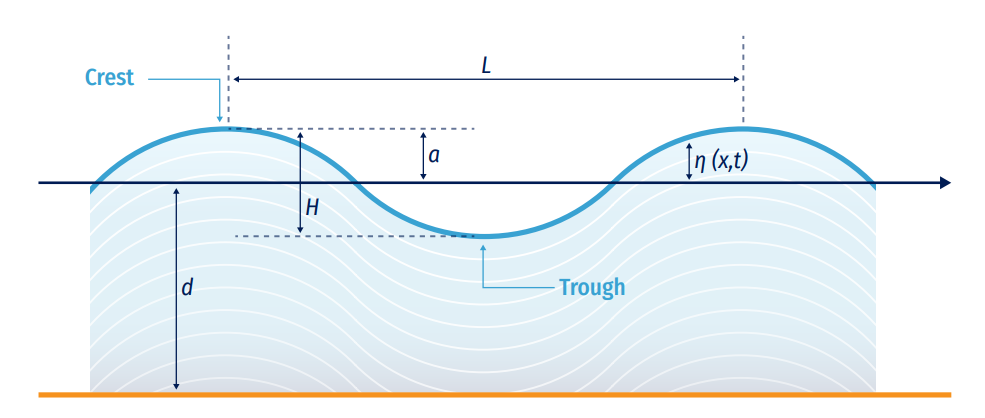
This scheme exemplifies ocean waves a as simple sinusoidal wave, where a represents the oscillatory and cyclic vertical distance between the mean water level and the crest height, and η(x,t) represents the vertical position of the free surface at a specific location x and time. The coordinate axis used to describe wave motion is located on the still water line z=0 and bottom of the water z=-d. Wavelength (L) can be defined using the dispersion relation (as described in Eq. 8.1), defined as the horizontal distance between two successive wave crests or troughs (wave lowest point) and directly related with the wave period (T, as the required time for two successive crests to pass from a fixed point in space or time respectively), over a water depth.

As waves propagate, water mass moves in orbital trajectories. Also, wave phase velocity or celerity (C), is equivalent to C=L/T.

This idealisation rarely appears in nature, neither in frequency nor in direction. Thus, irregular waves or real field waves can be organised as a superposition of a large number of sinusoidal components (monochromatic waves) going in multiple directions, each of them with different frequencies or periods, amplitudes and random phases. This idea allows the use of a classical Fourier analysis, statistical techniques, and well-known energy-spectral techniques to adequately assimilate and describe ocean waves that exist within any location and time window (generally within 1 hour as sea state definition).

Random or irregular ocean waves, as a summation of independent harmonic waves, can be described in detail with linear theory for surface gravity waves, only valid for small amplitude waves. Linear theory (also called Airy theory, or Airy waves), after a clear definition of basic governing equations and contour conditions, gives the solution of a long-crested harmonic propagating wave in the x-direction, as follows:

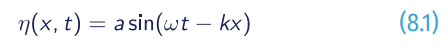
That yields the general dispersion equation that relates the angular frequency ω =2π/T and wavenumber ω =2π/L:

So, dispersion conditions can be used to calculate the wave propagation velocity at any depth, based only on the wave period. As a result, long waves travel faster compared to short waves. These waves, whose propagation speed depends on the wavelength and frequency, are called dispersive waves.

When waves travel and propagate in the ocean, they form groups of different components. Since the difference between the spectral sea-state frequencies is infinitely small (difference between adjacent wave numbers is also infinitely small), the velocity of the group (Cg ) can be calculated from the phase velocity (C) as shown below:

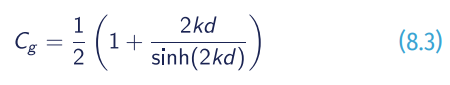
It indicates that the phase velocity (speed of an individual wave) is always equal or greater than the speed of the group. The dependence of the group velocity on frequency results in the disintegration of the wave groups: this is physically visible as longer waves travel faster ahead of the shorter waves and wave energy disperses across the ocean. A consequence of this is the transformation of an irregular sea (called SEA-type) created by a storm into a more regular and phase-ordered sea (or SWELL-type).

In the basic linear theory, these variables can define three zones that clearly differentiate the overall behaviour of waves as they are generated and propagated towards the coast, as follows:

• Deep water: limited by d>0.5 L where wave-induced velocities decrease exponentially with increasing distance from the surface. Water particles move in circles of decreasing radius towards the sea bottom. Eventually, the amplitude of the wave is equal to the radius of the biggest circle on the free surface. Individual waves of the group travel faster than the group.
• Shallow water: limited between d<0.05 L, for shallow waters, particle kinematics shows that the amplitude of the horizontal velocity is constant over the vertical axis and it does not depend on the depth; also the amplitude of the vertical velocity increases linearly from the seabed to the surface. The orbits of the particles in shallow waters are elliptic. The celerity (C) is calculated only by the depth (d) and the wavelength (L) is proportional to the wave period (T). Individual components travel at the same speed of the group, maintaining their position in the group.
• Intermediate depth: all other cases in which both water depth and period (or wavelength) have a significant influence on the solution of linear wave theory. In addition, individual waves of the group travel faster than the group (as in deep waters).

This definition of waves into different theoretical zones allows to classify the physical behaviour of the oscillatory flow in three categories: 

a. Wave generation in deep water by wind action; 
b. Wave propagation and dispersion from deep to intermediate waters;
c. Wave transformation and dissipation towards the coastal zone, and its interaction with bathymetry, natural and artificial structures.

The general knowledge of these processes allows understanding their degree of complexity, importance, and application in statistical or predictive climate systems. It is imperative to properly identify the experimental, mathematical or numerical tools to be selected to solve processes (based on the most relevant wave transformation characteristics), to generate a hierarchy of the variables and processes to be considered and to establish the hypotheses in assembling climate systems.

The following sections discuss these topics, with the purpose of enabling the setup of a climatic (multi-year) or predictive system for ocean waves from deep water to the coast, tailored to the processes that the user wants to include, considering pros and cons of each numerical module, as well as the inherent and concatenated uncertainties of the integrated system.

Ocean wind-generated waves are one of the most challenging research objects in meteo-oceanographic physics. They are generated and forced by the wind fields acting at global scale (Janssen, 2004, Chalikov, 2016) and are subject to important dissipation and strong nonlinear effects (Babanin, 2011), which drive the evolution of wave spectra at the scale of tens of thousands of wave periods (Hasselmann, 1962, Zakharov, 1968). Generation, dissipation, and interaction dynamics are the three main non-separable pillars for any wave model: once the waves are produced by the wind, no matter how small they are, the mechanisms of their attenuation and energy exchanges with other wave components within the wave spectrum are immediately activated. Moreover, each pillar is not a single physical process, but rather a plethora of various processes, often concurrent and with varying relative significance over the course of wave evolution.

The three main dynamics are always present but in particular circumstances, or from the point of view of a particular application, other processes can become relevant or even dominate. For example, various influences of surface currents (Babanin et al., 2017), sea ice (Thomson et al., 2018) or surface tension, as well as other forcings (Cavaleri et al., 2007).

In shallow-water environments and with extreme winds, waves become a different physical object and their respective wave models are notable for a lesser degree of physics and a larger degree of parametric and ad hoc tuning. For finite depths, dispersion is reduced or even ceases, nonlinearity grows but active nonlinear mechanisms change, balance between energy input and dissipation is no longer maintained, and a variety of new physical processes come into existence because of various wave-bottom interactions and sediment response (Young, 1999, Holthuijsen, 2007).

When winds exceed 30 m/s, a simultaneous change of physical regime takes place in all the three air-sea environments, i.e. atmospheric boundary layer, sea surface, and upper ocean (Babanin, 2018). For the waves on the ocean surface, this modifies wind input processes in which frequent flow separation and massive production of spray alters wind-wave exchanges and leads to the known effect of saturation of the sea drag. Wave breaking and dissipation are now driven by completely different dynamics, i.e. by direct wind forcing rather than nonlinear wave evolution.

Any ocean wave reanalysis (multi-year database) or prediction system, focusing on shallow waters of the coastal zone, will require detailed information on the most important processes involved in the transformation of ocean wave characteristics, which originated in deep water. This subsection presents a comprehensive description of these processes, their basic equations and the physics that need to be taken into account.

It is important to underline that the theories presented here treat each process as an isolated entity but, in reality, all these processes appear together and act concomitantly. Hence, it is necessary to create a hierarchy of the relevant processes for each sub-area of wave propagation towards the coast, so that developers of climate and forecasting systems can be aware and consider them appropriately.

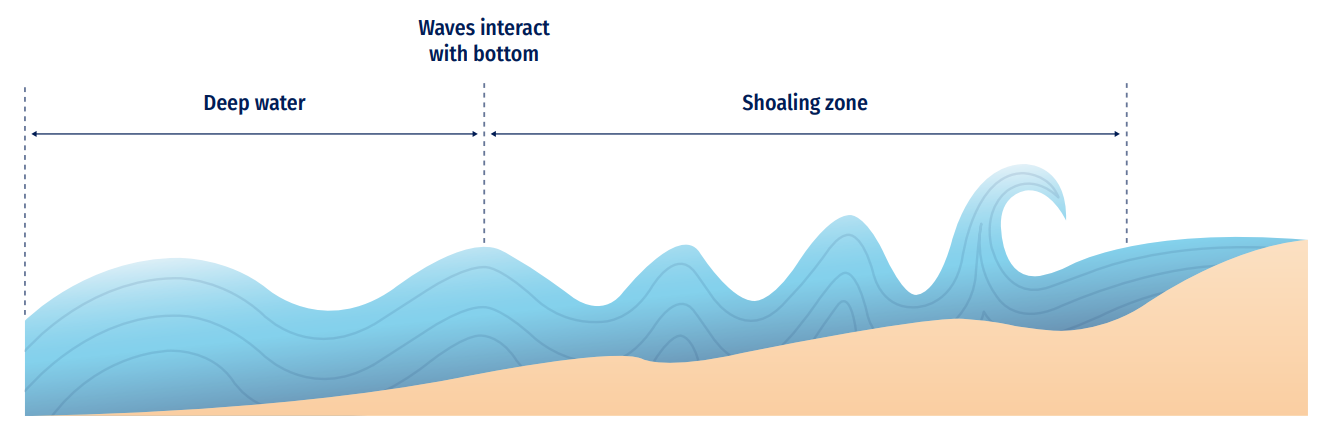
Shoaling happens when waves start to interact with the ocean's bottom or bathymetry configuration. As the wave propagates over intermediate and shallow waters zones, it reduces its celerity and maintains its frequency (linear theory main hypothesis); both wavelength and phase speed decrease, and wave amplitude trends to grow (Figure 8.10). In other words, in shallow waters, ocean waves become less dispersive, meaning that the phase speed is less dependent on the wave frequency.

The change in the wave height due to shoaling can be calculated from the following general relationship thorough a shoaling coefficient, K_s:

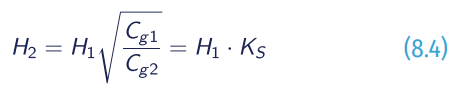
In practice, wave shoaling phenomena can be observed as a local increase of wave heights due the reduction of the bathymetry profile or depths. Also can occur also in a reverse form, i.e. shoaled waves travelling into progressively deeper water. This results in a wavelength increase effect (wave speed also increases), while wave height decreases.

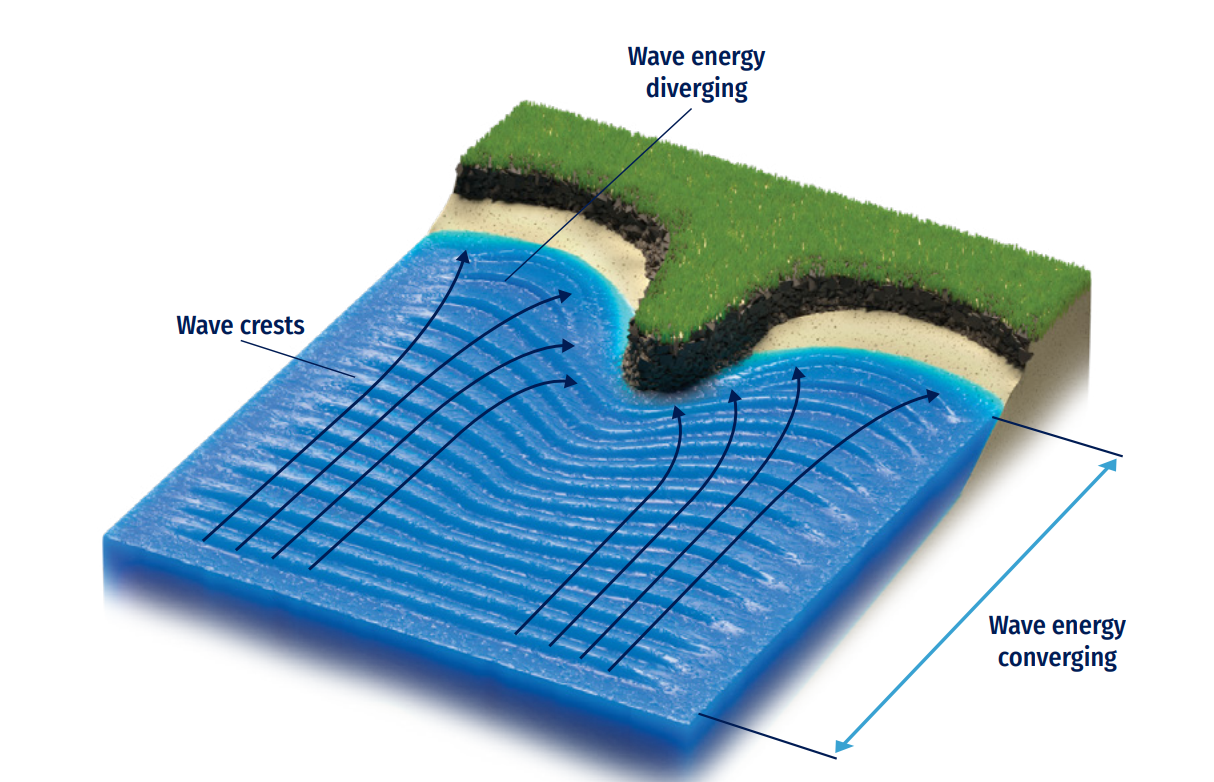
When ocean waves change their direction of propagation from the bottom or for a bathymetry interaction, a refraction occurs, mainly due to the change of a same wave front travelling at different bathymetric depths, yielding partial reduction of its celerity. One section of a travelling wave moves faster than the other part, resulting in the wave fronts turning towards the coast (Figure 8.11). Ocean waves will always turn towards the region with lower propagation speed. Physically, wave refraction satisfies Snell’s law:

As waves propagate towards a coast, waves crests tend to become parallel to the coastline. Refraction can be visualised as the gradual change in waves’ direction when they tend to approach a coastline at an angle 0°, known as oblique incidence.

Additionally, refraction can have an important effect (partial wave height reduction or increase) calculated with a refraction coefficient (KR) as follows:

Finally, combined wave refraction and shoaling are always present simultaneously and affect wave height as follows:

When ocean waves reach and interact with any structure (natural or artificial, totally or partially emerged), wave diffraction occurs, which is described as the blocking and spreading of energy laterally perpendicular to the dominant direction of wave propagation. The result is that wave fronts, angles, and energy spreads behind (so-called lee side) the obstacle and wave heights appear lower in sheltered areas (Figure 8.12). Also, wave fronts rearrange into more structured and radial/focused wave propagation patterns.

The circular pattern adopted by diffracted wave crests, as they penetrate in the lee side of obstacles, diminishes rapidly as waves are diffracted further behind the obstacles. This behaviour could be relevant for any OOFS near bays, harbours, islands, and peninsulas areas.

Diffracted waves are also still affected with both refraction and shoaling effects, especially for large sheltered zones with relevant bathymetric changes. Also, semi-diffraction effects can occur for those semi-submerged structures (breakwaters and/or steep bathymetric bodies) with a clear refraction-diffraction combined effect.

Analytical solution for diffracted waves can be handled through a diffraction coefficient for an idealised constant bathymetry and semi-infinite emerged bodies (CERC, 1984), ignoring wave reflection effects, and using instead graphical diagrams as a function of the wavelength, the angle of incidence between the emerged body and the distance between the head of the breakwater and the point of calculation (Koutitas, 1990). For more realistic configuration, numerical approaches (phase averaging or resolving strategies) should be invoked.

Ocean waves are also affected by currents (tides, storm surges, river discharges, ambient currents, etc.). Changes in the amplitude, frequency, and direction of the incident waves are expected (Dean and Dalrymple, 1991).

Current-derived local shoaling might occur if waves get blocked by a current. Also, current-induced refraction can induce changes in the direction of speed/wave propagation, as well as energy exchange between the current and the wave can be present at coastal/mouth of the river zones and in some harbour entrances affected by littoral currents (Figure 8.13).

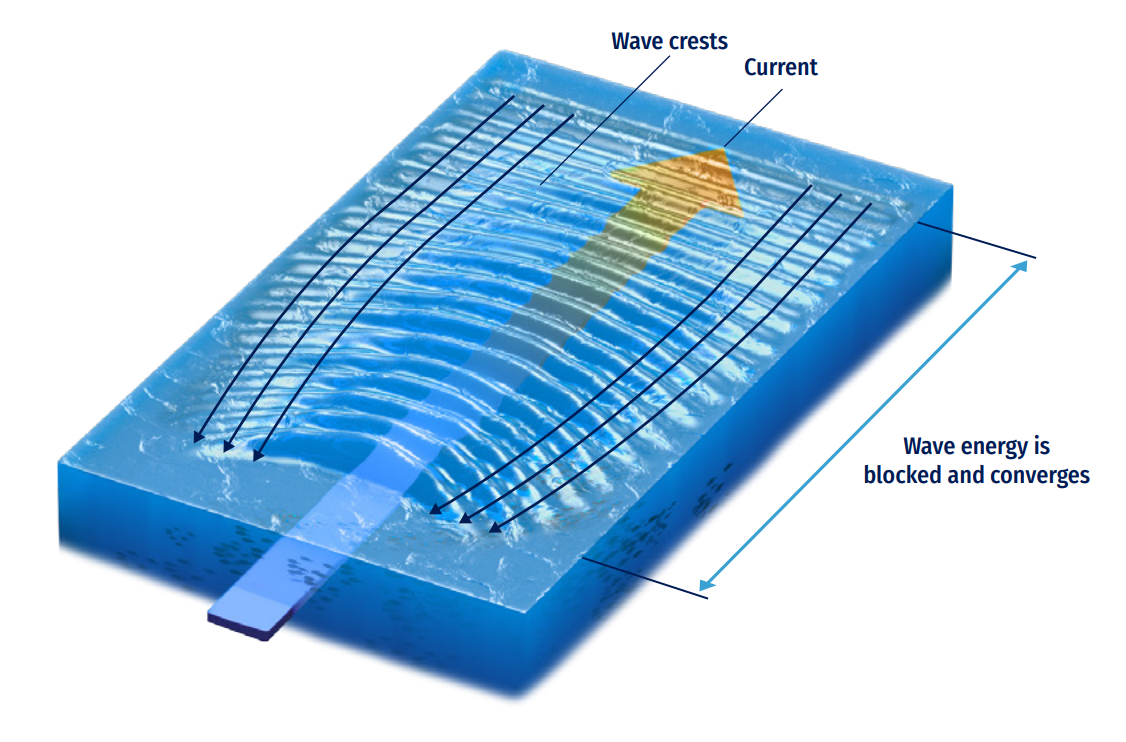
Linear theory is still valid and dispersion equation can be adapted to take into account currents (vertical integrated depth) as follows:

Where U_n is the component of the current in the wave direction.

Wave breaking is maybe one of the most energy-dissipating phenomena that waves can experience. It occurs when a shoaling/growing wave propagates over a limited depth profile, reaching its own water volume stability. As waves propagate towards shallow water, they become steeper until a stability-limit when they break, generating a complex mechanism related to fluid turbulence and vorticity.

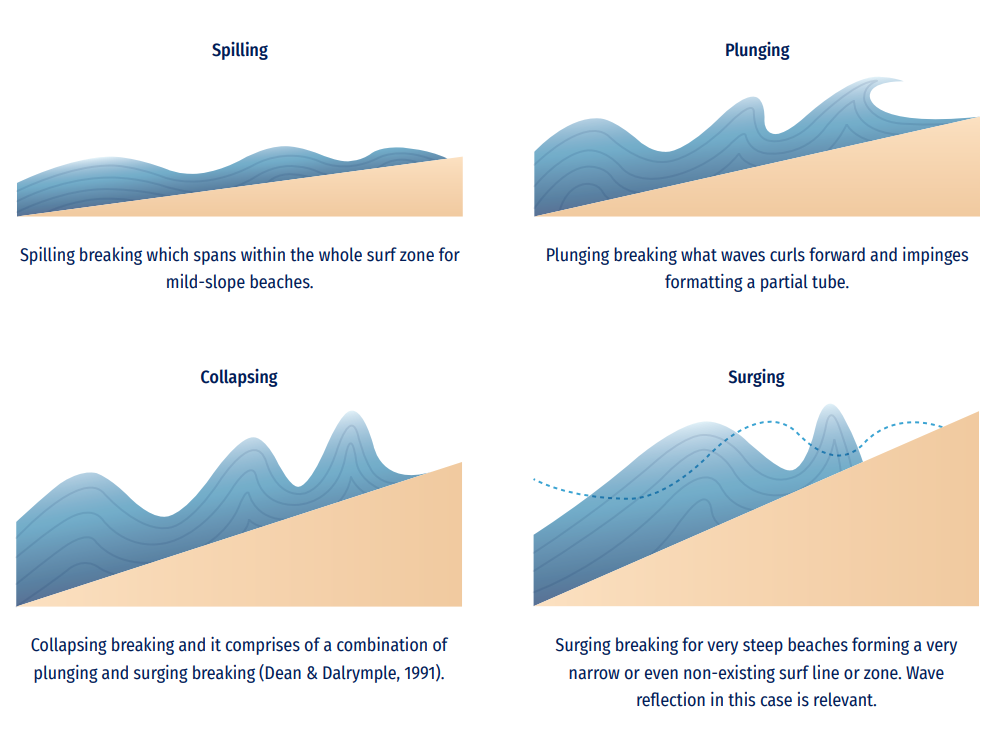
Depending on water wave incoming characteristics such as frequency, direction, and height, and the bathymetric characteristics (slope), different types of wave breaking are expected to occur. A parameter called the Iribarren number (also known as surf similarity parameter) can be employed for these classifications (see Figure 8.14), defined as a function of the bottom gradient and wave steepness as:

Where _α is the bottom slope, H is the incident wave height and L_o is the deep-water wavelength. 

A simple way to estimate breaking limit depth is based on the breaking height equal to a fraction of the water depth, as established by McCowan (1984):

Where k=0.78.

For coastal wave climate or forecast applications, realistic characterization of wave breaking could be one of the most challenging issues and should be handled numerically when dealing with prediction of structure damaged by waves inside the surf zone of the breaker line at beach profile.

Additionally, wave dissipation due to bottom friction can be relevant when waves propagate into shallow water. Friction between the bottom and the orbital motion of water wave particles dissipates wave energy; it depends on both the orbital velocity and the roughness of the bottom.

As wave fronts reach any coastal obstacle, part of the total-incident wave energy travels back into the open sea, basin, or sheltered area (Figure 8.15). Some of the original wave energy is reflected and some is dissipated. The amount of energy is reflected (stated as reflection coefficient or K_f) depending on both the vertical structure typology (natural cliffs, beaches, artificial breakwaters, quays, etc.) and the incident wave characteristics (mainly due to wave frequency).

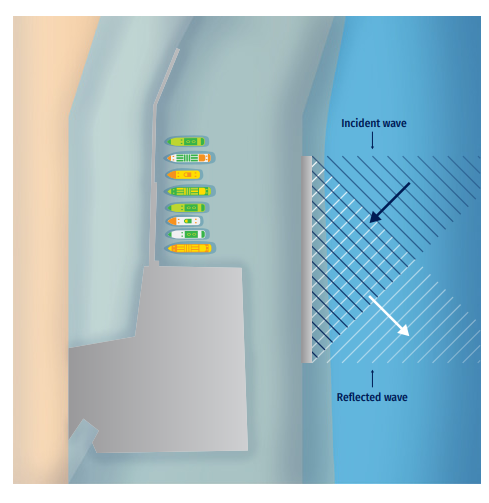
An idealised vertical structure can reflect a 100% of the incoming wave energy (K_R=1) but in real imperfect coastal perimeters this value is commonly below (K_f<1), due to the combination of complex physical processes (e.g. wave breaking, friction, percolation, run-up, etc.) that occur in the structure-water interface.

For shallow water zones adjacent to coastal structures, it is important to include wave reflection in the list of relevant wave transformation processes, especially for those wave climate or forecast systems that needs a good characterization for both incident and reflected waves at the study zone (i.e. propagation of collateral reflection effects from far areas such harbours, cliffs, reefs, jetties, harbour agitation, etc.).

The mathematical description of wave reflection deals with the calculation of wave motion as a linear sum of the incident wave and the (partially) reflected wave, as a transient or standing wave effect (for a constant deep domain and 1D approach). This can be complex for real bathymetry and coastal perimeter configuration, when irregular wave trains interact with different structures and coastal typologies and, in this case, an ad-hoc numerical approach should be used.

Partial wave reflection can also be relevant for semi-submerged structures and/or steep bathymetric changes (e.g. dredged navigation channels), as it interacts with wave shoaling, diffraction, and refraction effects. For example, harbour agitation phenomena deal with a complex computation of diffracted and partially reflected wave patterns.

Along with wave reflection effect and wave breaking on coasts and rubble-mound structures, waves’ energy and frequencies can overtop these elements, tide instants, and each particular structure's typologies and characteristics.

Within wave climate or forecast systems, for a detailed definition of wave effects interaction with coastal structures (natural or artificial) could be important: i) wave run-up height, defined as (Ru2%) the wave level, measured vertically from the still water line which is exceeded by 2% of the number of incident waves; and ii) wave overtopping discharge (Figure 8.16), defined as the average water discharge per linear metre of width of the structure.

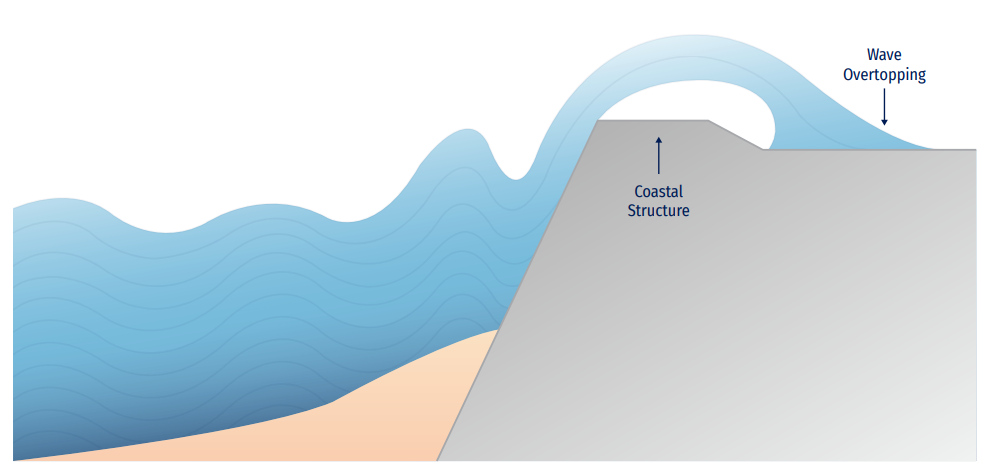
In recent times, forecast systems dealing with wave overtopping along a pedestrian coastal zone are delivered worldwide. The precision of these early-alert systems depends on a good reproduction of both incoming water waves and the geometry of the structure (freeboard, crest width, roughness, slope, permeability, and porosity). In order to calculate these derived variables, EurOtop Manual (Van der Meer et al., 2016) gathered some empirical formulae to easily obtain them. Also, some advanced numerical models (based on Computational Fluid Dynamics) are available to obtain, with a very good approximation, overtopping values and discharge volumes (Losada et al., 2008).