COORDINATORS
Wave models provide at each grid point two-dimensional wave spectrum F(f,θ), which describes how the wave energy is distributed as a function of frequency f and propagation direction θ. In general, the wave spectrum F is discretized in 30 frequencies and 24 directions. To simplify the study of wave conditions, integrated parameters are derived from weighted integrals of F(f,θ). The moment of order n, mn is defined as the following integral:
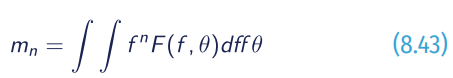
The integrations are performed over all frequencies and directions or over a spectral subdomain when the spectrum is split between wind sea and swell or partitioned into main components. The wind sea wave component is subject to the wind forcing, and then wave phase speed is smaller than the wind speed at the ocean surface. The remaining part is considered swell. It is established in the WAM model for instance, the spectral energy is subject to wind forcing when the following approximation is satisfied:
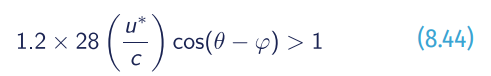
where u∗ is the friction velocity, c is the phase speed as derived from the linear theory of waves and φ is the wind direction. The integrated parameters are therefore also computed for wind waves and swell by only integrating over the respective components of F(f,θ) that satisfies 8.43 or not.
Significant wave height
The wave energy is the 0th order of the moment m0 and significant wave height (Hs) is defined as follows (Hs snapshot shown in Figure 8.38):


Mean period
The mean period (snapshot in Figure 8.39) is expressed in several ways. The most used is Tm-1 which is based on the moment of order -1, that is

Tm-1 is also commonly known as the energy mean wave period. By considering Hs, it can be used to determine the wave energy flux per unit of wave-crest length in deep water, also indicated as the wave power per unit of wave-crest length P.
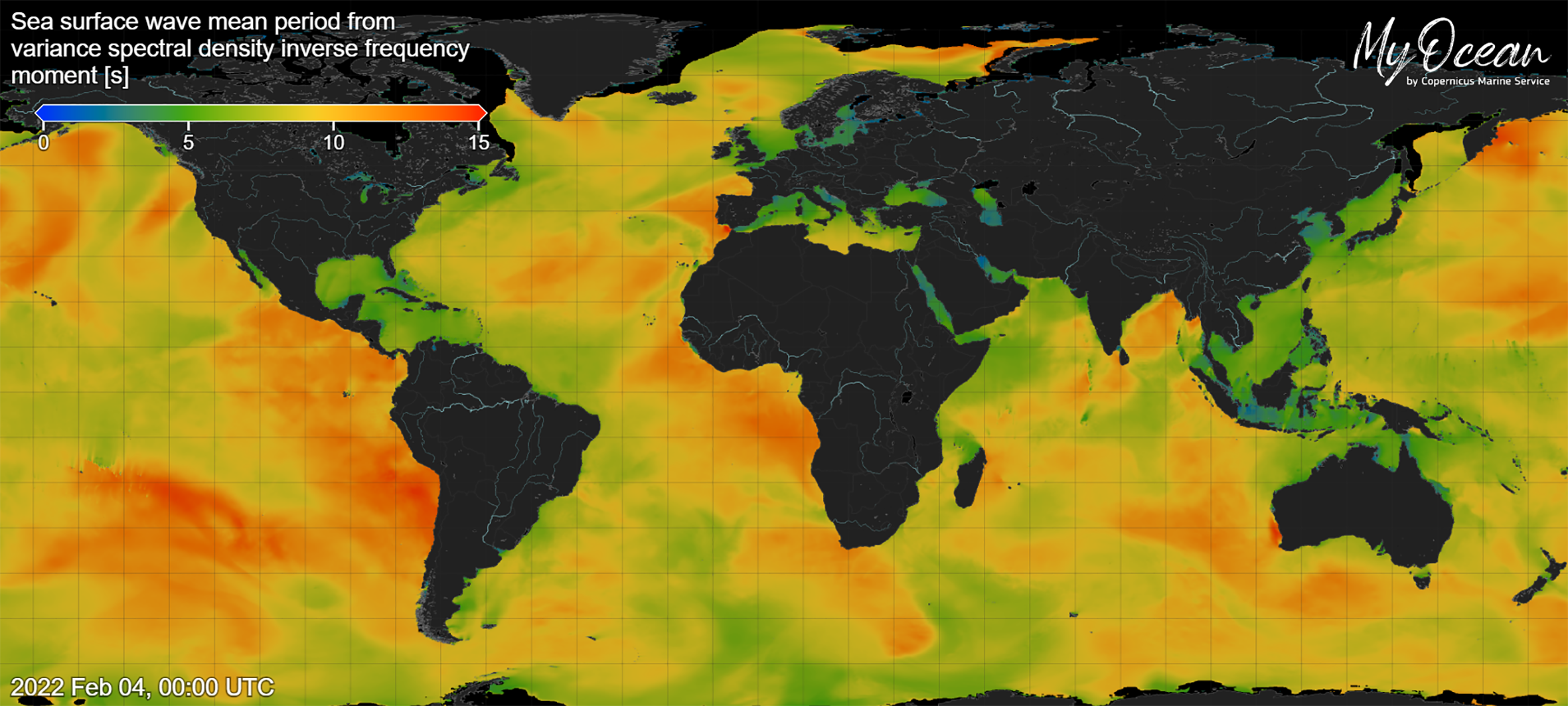
To analyse different aspects of the wave field, other moments can be used to define a mean period. Periods can be based on the first moment Tm1 given by:

Tm1 is essentially the reciprocal of the mean frequency. It can be used to estimate the magnitude of Stokes drift transport in deep water and periods based on the second moment Tm2 given by:

Tm2 is also known as the zero-crossing mean wave period, as it corresponds to the mean period that is determined from observations of the sea surface elevation using the zero-crossing method.
Peak period
The peak period is defined for total sea and can be expressed as the reciprocal peak frequency of the 1D wave spectrum F(f) integrated over directions. There is a second way to compute the peak frequency and it is obtained from a parabolic fit around the discretized maximum of the two-dimensional wave spectrum F(f,θ).
Mean wave direction
The mean wave direction is defined by weighting the wave spectrum F(f,θ). It is expressed as follows:
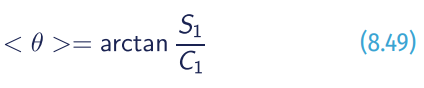
where S1 is the integral of sin(θ)*F(f,θ) over frequencies and directions, while C1 is the integral of cos(θ)*F(f,θ) over f and θ.
Directional spread
The wave directional spread gives the information on the directional distribution of the total sea, or it can be applied for different wave components. It is expressed as follows:

where M is I/m0 and I is the integral of cos(θ-<θ>)*F(f,θ) over f and θ. <θ> is the mean direction. The directional spread can be computed for wind, sea, and swell components.
Surface Stokes Drift
The Stokes drift impacts the turbulence in the upper ocean layers and contributes to the source of energy of the ocean circulation, particularly the Langmuir circulation. The surface Stokes drift Us is computed from the wave spectrum in deep water by the following relation:
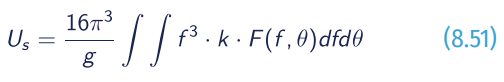
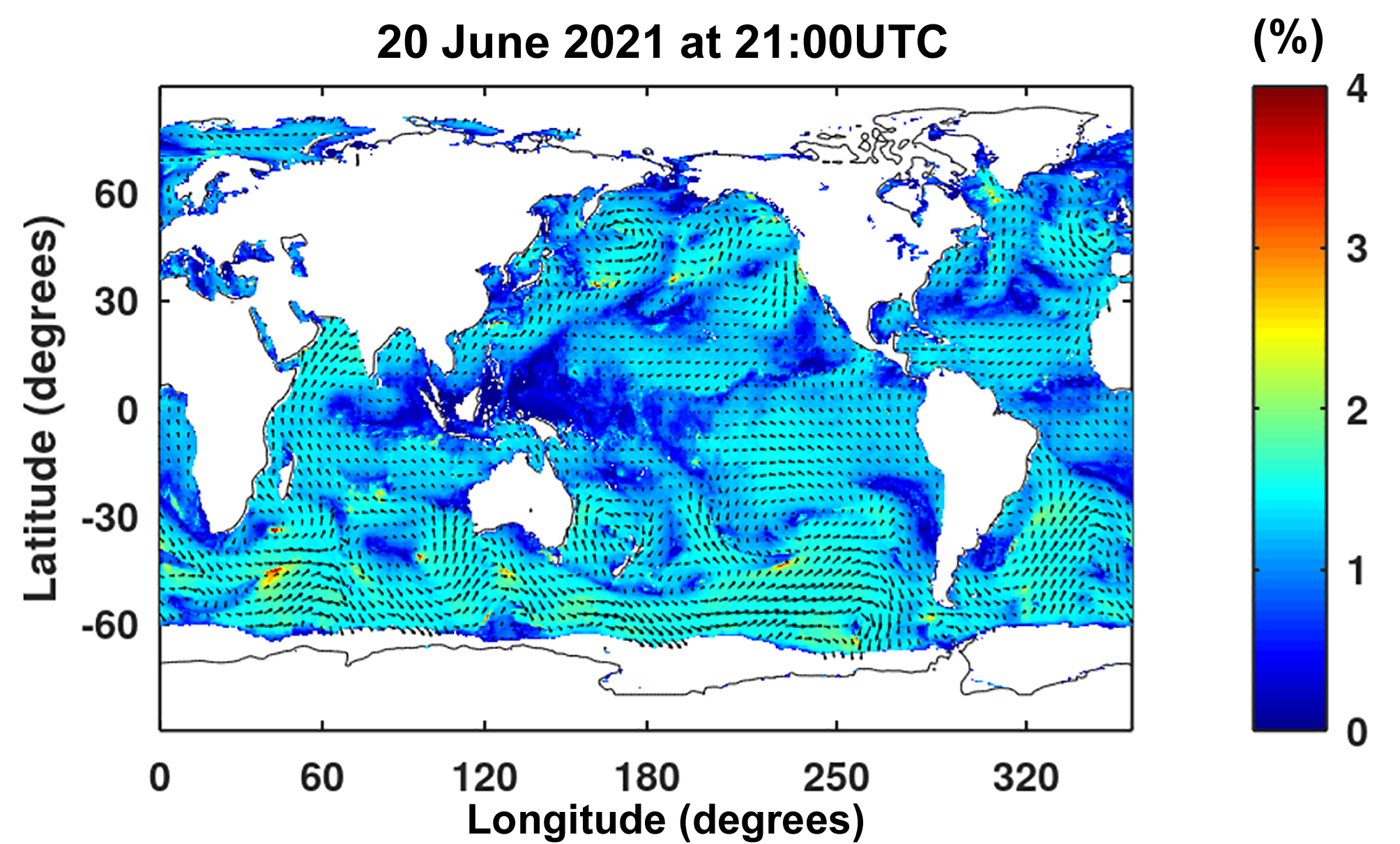
where the integration is over all frequencies and directions. k is the unit vector in the direction of the wave component. In the high frequency range, the Phillips spectral shape is used with accounting of spectral level of the last frequency bin. Figure 8.40 shows the ratio of Stokes drift magnitude to 10 m wind speed.
Partitioning wave spectrum
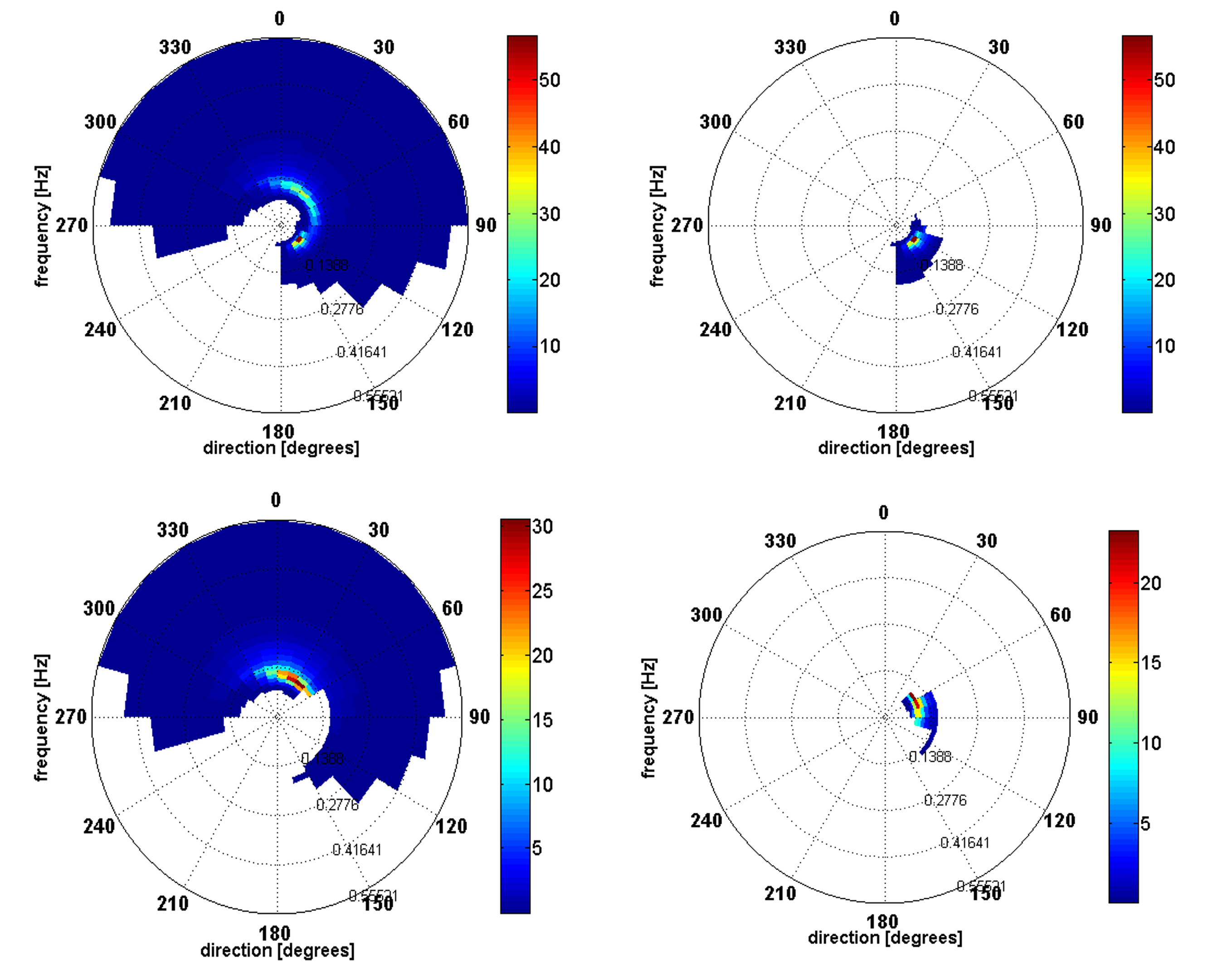
In general, wave forecasters firstly analyse the integrated parameters over the full wave spectrum describing the total sea. Then, they refine their analysis by examining the different dominant wave trains representing wind, sea, and swell. Most wave models include a partitioning procedure, which aims to separate the different wave systems represented by energy peaks in the wave spectrum. The most used partitioning procedure is adapted from Hanson and Phillips (2002) and is based on the watershed method inspired from image processing. After splitting the wind sea and swell wave spectrum, the method consists in identifying the energy peaks in the wave spectrum and isolating a partition with decreasing energy from the peak to a limit corresponding to an increase in energy. Several partitions or wave systems can be detected in a wave spectrum, and they are classified by decreasing order of their wave height. An example of partitioning is shown in Figure 8.41, where three partitions are detected with two swells and one wind sea. The average height, period and direction can be calculated on each partition.
Wave energy flux
The wave energy flux per unit of wave-crest length in deep water can be computed by using the wave period Tm-1 and significant wave height Hs:
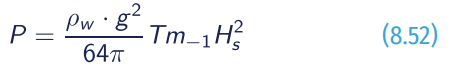
where rw is the water density and g is the acceleration due to gravity.
The wave energy flux can be expressed by integrating the flux of each spectral component.
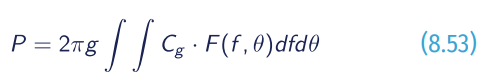
where Cg is the group velocity in deep water.
Numerical models for wave generation and propagation can provide different variables to be used in multi-year and predictive systems. Table 8.1 lists variables that are commonly provided by numerical and that may be of special relevance for users, as well as for developers who wish to set up future wave OOFS and multi-year systems.
Common variable names (usually provided by third-generation spectral wave model and/or a mild slope approximations) | Symbol | Units |
|---|---|---|
| Significant wave height | Hs | m |
| Peak period | Tp | s |
| Mean wave period | Tm | s |
| Mean and Peak wave direction | Ө | °N |
| Complete wave spectra matrix | S | m²/Hz/ºN |
| Mean parameters of wave partitions (Hs,Tm,Tp and Dir) for: 2 Swells and 1 wind sea | Hsi, Tpi, Diri | m, s, ºn |
| Maximum wave height | Hmax | m |
| Maximum wave period | Tmax | m |
| Meridional component of Stokes drift | Us | m/s |
| Zonal component of Stokes drift | Vs | m/s |
| Drag coefficient with waves | Cd | |
| Normalised stress to ocean | Tauoc | |
| Mean square slope | mss |
Advanced variable names (usually provided by phase resolving models and CFD approaches) | Symbol | Units |
|---|---|---|
| Free-surface time series at points and maps | η | m |
| Wave breaking-induced currents | U-V | m/s |
| Instantaneous wave run-up | Ru | m |
| Instantaneous wave overtopping volume | q | m³/s per m |
| Infragravity wave oscillations | ηIG | m |
| Multi-directional wave spectra matrix (agitation) | S | m ²/Hz/ºN |
| Instantaneous wave pressures over structures | P | N/m² |
| Instantaneous forces over structures | F | N |
| Instantaneous wave currents | u-v | m/s |
Table 8.1. Common names of wave variables.
References

Álvarez-Fanjul, E., García-Sotillo, M., Pérez Gómez, B., García Valdecasas, J. M., Pérez Rubio, S., Rodríguez Dapena, A., et al. (2018). Operational oceanography at the service of the ports. In: “New Frontiers in Operational Oceanography”, Editors: E. Chassignet, A. Pascual, J. Tintoré, and J. Verron (Cambridge: GODAE OceanView), 729-736, https://doi.org/10.17125/gov2018.ch27
Alves, J.-H.G.M., Wittmann, P., Sestak, M., Schauer, J., Stripling, S., Bernier, N.B., Mclean, J., Chao, Y., Chawla, A., Tolman, H., Nelson, G., and Klotz, S. (2013). The NCEP–FNMOC combined wave ensemble product: expanding benefits of inter-agency probabilistic forecasts to the oceanic environment. Bulletin of the American Meteorological Society, 94(12), 1893-1905, https://doi.org/10.1175/BAMS-D-12-00032.1
Aouf, L., Hauser, D., Law-Chune, S., Chapron, B., Dalphinet, A., and Tourain, C. (2021). New directional wave observations from CFOSAT: impact on ocean/wave coupling in the Southern Ocean. EGU General Assembly 2021, online, 19-30 Apr 2021, EGU21-7412, https://doi.org/10.5194/egusphere-egu21-7412
Aouf, L., Lefèvre, J., and Hauser, D. (2006). Assimilation of Directional Wave Spectra in the Wave Model WAM: An Impact Study from Synthetic Observations in Preparation for the SWIMSAT Satellite Mission. Journal of Atmospheric and Oceanic Technology, 23(3), 448-463, https://doi.org/10.1175/JTECH1861.1
Aouf, L., Danièle, H., Céline, T., Bertrand, C. (2018). On the Assimilation of Multi-Source of Directional Wave Spectra from Sentinel-1A and 1B, and CFOSAT in the Wave Model MFWAM: Toward an Operational Use in CMEMS-MFC. IGARSS 2018 - 2018 IEEE International Geoscience and Remote Sensing Symposium, 2018, pp. 5663-5666, doi:10.1109/IGARSS.2018.8517731
Ardhuin, F., Otero, M., Merrifield, S., Grouazel, A., and Terril, E. (2020). Ice breakup controls dissipation of wind waves across Southern Ocean sea ice. Geophysical Research Letters, 47, e2020GL087699. https://doi.org/10.1029/2020GL087699
Ardhuin, F., Rogers, E., Babanin, A., Filipot, J.-F., Magne, R., Roland, A., van der Westhuysen, A., Queffeulou, P., Lefevre, J.-M., Aouf, L., Collard, F. (2010). Semi-empirical dissipation source functions for ocean waves. Part I: definitions, calibration and validations. Journal of Physical Oceanography, 40, 1917-1941, https://doi.org/10.1175/2010JPO4324.1
Babanin, A.V. (2011). Breaking and Dissipation of Ocean Surface Waves. Cambridge University Press, 480 p.
Babanin, A.V. (2018). Change of regime of air-sea dynamics in extreme Metocean conditions. Proceedings of the ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering OMAE2018, June 17-22, 2018, Madrid, Spain, paper 77484, 6 p.
Babanin, A.V., Onorato, M., and Qiao, F. (2012). Surface waves and wave-coupled effects in lower atmosphere and upper ocean. Journal of Geophysical Research: Ocean, 117(C11), https://doi.org/10.1029/2012JC007932
Babanin, A.V., van der Westhuysen, A., Chalikov, D., and Rogers, W.E. (2017). Advanced wave modelling including wave-current interaction. In “The Sea: The Science of Ocean Prediction”, Eds. Nadia Pinardi, Pierre F. J. Lermusiaux, Kenneth H. Brink and Ruth Preller, Journal of Marine Research, 75, 239-262.
Barstow, S., Mørk, G., Lønseth, L., and Schjølberg, P.. (2004). Use of satellite wave data in the world waves project. Gayana (Concepción), 68(2, Supl.TIProc), 40-47, http://dx.doi.org/10.4067/S0717-65382004000200007
Battjes, J.A., and Janssen, P.A.E..M. (1978). Energy Loss and Setup Due to Breaking in Random Waves. Proceedings of 16th Coastal Engineering Conference, Hamburg, Germany, 569-587.
Bauer, E., Hasselmann, S., Hasselmann, K. and Graber, H. C. (1992). Validation and assimilation of Seasat altimeter wave heights using the WAM wave model. Journal of Geophysical Research: Ocean, C97, 12671-12682, https://doi.org/10.1029/92JC01056
Berkhoff, J. C. (1972). Computation of combined refraction-diffraction. 13th International Conference on Coastal Engineering, (pp. 471-490). ASCE.
Beven J. (2019). Hurricane Pablo tropical cyclone report, NHC-NOAA.
Bidlot J. R. (2016). Twenty-one years of wave forecast verification. ECMWF Newsletter, 150, 2016.
Booij, N., Ris, R., and Holthuijsen, Leo. (1999). A third-generation wave model for coastal regions, Part I, Model description and validation. Journal of Geophysical Research: Ocean, 104. 7649-7656, https://doi.org/10.1029/98JC02622
Breivik, L-A., Reistad, M., Schyberg, H., Sunde, J., Krogstad, H. E., and Johnsen, H. (1998). Assimilation of ERS SAR wave spectra in an operational wave model. Journal of Geophysical Research: Ocean, 103, 7887- 7900, https://doi.org/10.1029/97JC02728
Breivik, Ø., Gusdal, Y., Furevik, B.R., Aarnes, O.J., Reistand, M. (2009). Nearshore wave forecasting and hindcasting by dynamical and statistical downscaling. Journal of Marine Systems, 78, S235-S243, https://doi.org/10.1016/j.jmarsys.2009.01.025
Breivik, Ø., Mogensen, K., Bidlot, J.-R., Balmaseda, M. A., and Janssen, P. A. E. M. (2015), Surface wave effects in the NEMO ocean model: Forced and coupled experiments. Journal of Geophysical Research: Ocean, 120, 2973-2992, https://doi.org/10.1002/2014JC010565
Brocchini, M. (2013). A reasoned overview on Boussinesq-type models: the interplay between physics, mathematics and numerics. Proceedings of the Royal Society A Mathematical, Physics and Engineering Science, 469, https://doi.org/10.1098/rspa.2013.0496
Browne, M., Castelle, B., Strauss, D., Tomlinson, R., Blumenstein, M., Lane, C. (2007). Near-shore swell estimation from a global wind–wave model: spectral process, linear and artificial neural network models. Coastal Engineering, 54, 445-460, https://doi.org/10.1016/j.coastaleng.2006.11.007
Bunney, C., and Saulter, A. (2015). An ensemble forecast system for prediction of Atlantic-UK wind waves. Ocean Modelling, 96(1), 103-116, doi: 10.1016/j.ocemod.2015.07.005
Dean, R. G., Dalrymple, R. A. (1991). Water wave mechanics for engineers and scientists (Advanced series on ocean engineering - Volume 2), Singapore World Scientific Publishing.
Camus, P., Mendez, F., Medina, R. (2011). A hybrid efficient method to downscale wave climate to coastal areas. Coastal Engineering, 58(9), 851-862, https://doi.org/10.1016/j.coastaleng.2011.05.007
Camus, P., Mendez, F.J., Medina, R., Tomas, A., Izaguirre, C. (2013). High resolution downscaled ocean waves (DOW) reanalysis in coastal areas. Coastal Engineering, 72, 56-68, https://doi.org/10.1016/j.coastaleng.2012.09.002
Cavaleri, L., Alves, J.-H.G.M., Ardhuin, F., Babanin, A., Banner, M., Belibassakis, K., Benoit, M., Donelan, M., Groeneweg, J., Herbers, T.H.C., Hwang, P., Janssen, P.A.E.M., Janssen, T., Lavrenov, I.V., Magne, R., Monbaliu, J., Onorato, M., Polnikov, V., Resio, D., Rogers, W.E., Sheremet, A., McKee Smith, J., Tolman, H.L., van Vledder, G., Wolf, J., Young, I. (2007). Wave modeling - the state of the art. Progress in Oceanography, 75(4), 603-674, https://doi.org/10.1016/j.pocean.2007.05.005
Cavaleri, L., Abdalla, S., Benetazzo, A., Bertotti, L., Bidlot, J.-R., Breivik, Ø., Carniel, S., Jensen, R.E., Portilla-Yandun, J., Rogers, W.E., Roland, A., Sanchez-Arcilla, A., Smith, J.M., Staneva, J., Toledo, Y., van Vledder, G.Ph., and van der Westhuysen, A.J. (2018). Wave modelling in coastal and inner seas. Progress in Oceanography, 167, 164-233, https://doi.org/10.1016/j.pocean.2018.03.010
CERC, (1984). Shore Protection Manual. Department of the Army US. Army Corps of Engineers, Washington DC.
Chalikov, D. (2016). Numerical Modeling of Sea Waves. Springer, 330 p.
Chelton, D. B., and McCabe, P. J. (1985). A review of satellite altimeter measurement of sea surface wind speed: with a proposed new algorithm. Journal of Geophysical Research: Oceans, 90(3), 4707-4720, https://doi.org/10.1029/JC090iC03p04707
Chen, H.S. (2006). Ensemble Prediction of Ocean Waves at NCEP. Proceedings of 28th Ocean Engineering Conference, Taiwan.
Climate Change Initiative Coastal Sea Level Team(The).(2020). Coastal sea level anomalies andassociatedtrends from Jason satellite altimetry over 2002-2018. Scientific Data, 7, 357, https://doi.org/10.1038/s41597-020-00694-w
Dean, R. G., and Dalrymple, R. A. (1991). Water wave mechanics for engineers and scientists. In: “Advanced Series on Ocean Engineering: Volume 2” by R.G. Dean and R.A. Dalrymple, World Scientific Publishing Co Pte Ltd, https://doi.org/10.1142/1232
Derkani, M. H., Alberello, A., Nelli, F., Bennetts, L.G., Hessner, K. G., MacHutchon, K., Reichert, L., Aouf, L., Khan, S., Toffoli, A. (2021). Wind, waves, and surface currents in the Southern Ocean: observations from the Antarctic Circumnavigation Expedition. Earth System Science Data, 13, 1189-1209, https://doi.org/10.5194/essd-13-1189-2021
Dingemanns, M. (1997). Waterwave propagation over uneven bottoms. Advanced Series on Ocean Engineering, 13(2), 967.
Donelan, M., Haus, B.K., Reul, N., Plant, W., Stiassnie, M., Graber, H.C., Brown, O., Saltzman, E. (2004). On the limiting aerodynamic roughness of the ocean in very strong winds. Geophysical Research Letters, 31(18), https://doi.org/10.1029/2004GL019460
Durrant, T.H., Woodcock F., and Greenslade, D.J.M. (2009). Consensus forecasts of modelled wave parameters. Weather and Forecasting, 24, 492-503, https://doi.org/10.1175/2008WAF2222143.1
Ebert, E. (2001). Ability of a poor man’s ensemble to predict the probability and distribution of precipitation. Monthly Weather Review,129(10), 2461–2480, https://doi.org/10.1175/1520-0493(2001)129<2461:AOAPMS>2.0.CO;2
Ebert, E.E. (2008). Fuzzy verification of high resolution gridded forecasts: A review and proposed framework. Meteorological Applications, 15, 51-64, https://doi.org/10.1002/met.25
Eckart, C. (1952). The propagation of gravity waves from deep to shallow water. Circular 20, National Bureau of Standards, 165-173.
Edson, J.B., Jampana, V., Weller, R.A., Bigorre, S.P., Plueddemann, A.J., Fairall, C.W., Miller, S.D., Mahrt, L., Vickers, D., and Hersbach, H. (2013). On the exchange of momentum over the open ocean. Journal of Physical Oceanography, 43(8), 1589-1610, https://doi.org/10.1175/JPO-D-12-0173.1
Fengyan, S., Kirby, J. T., Tehranirad, B., Harris, J. C., and Grilli, S. (2012). FUNWAVE-TVD: Fully Nonlinear Boussinesq Wave Model with TVD Solver. Documentation and User’s Manual (Version 2.0). Center for Applied Coastal Research, University of Delaware, Newark, DE. Available at: https://www1.udel.edu/kirby/papers/shi-etal-cacr-11-04-version2.0.pdf
Gaslikova, L., Weisse, R. (2006). Estimating near-shore wave statistics from regional hindcasts using downscaling techniques. Ocean Dynamics, 56, 26-35, https://doi.org/10.1007/s10236-005-0041-2
Greenslade, D.J.M. and Young, I.R. (2004). Background errors in a global wave model determined from altimeter data. Journal of Geophysical Research: Oceans, 109(C9), https://doi.org/10.1029/2004JC002324
González-Marco, D., Sierra, J. P., Ybarra, O. F., Sánchez-Arcilla, A. (2008). Implications of long waves in harbour management: The Gijón port case study. Ocean & Coastal Management, 51(2), 180-201, https://doi.org/10.1016/j.ocecoaman.2007.04.001
Groeneweg, J., Ledden, M., Zijlema, M. (2007). Wave transformation in front of the Dutch Coast. Proceedings of the Coastal Engineering Conference, 552-564, https://doi.org/10.1142/9789812709554_0048
Gulev, S. K., Grigorieva, V., Sterl, A., and Woolf, D. (2003). Assessment of the reliability of wave observations from voluntary observing ships: Insights from the validation of a global wind wave climatology based on voluntary observing ship data. Journal of Geophysical Research: Oceans, 108(C7), https://doi.org/10.1029/2002JC001437
Hanley, K.E., Belcher, S.E., and Sullivan, P.P. (2010). A global climatology of wind-wave interaction. Journal of Physical Oceanography, 40, 1263-1282, https://doi.org/10.1175/2010JPO4377.1
Hanson, J. L., Phillips, O. M. (2001). Automated Analysis of Ocean Surface Directional Wave Spectra. Journal of Atmospheric and Oceanic Technology, 18(2), 277-293, https://doi.org/10.1175/1520-0426(2001)018<0277:AAOOSD>2.0.CO;2
Hansom, J. et al. (2015). Extreme Waves: Causes, Characteristics and Impact on Coastal Environments and Society January 2015. In: “Coastal and Marine Hazards, Risks, and Disasters”, Edition: Hazards and Disasters Series, Elsevier Major Reference Works, Chapter 11: Extreme Waves: Causes, Characteristics and Impact on Coastal Environments and Society. Publisher:; Elsevier; Editors: Ellis, J and Sherman, D. J.
Hasselmann, K. (1962). On the non-linear energy transfer in a gravity-wave spectrum part 1. General theory. Journal of Fluid Mechanics, 12 (4), 481-500.
Hasselmann, K., Barnett, T. P., Bouws, E., Carlson, H., Cartwright, D. E., Enke, K., Ewing, J. A.,Gienapp, H., Hasselmann, D. E., Kruseman, P., Meerburg, A., M¨uller, P., Olbers, D. J., Richter, K., Sell, W. and Walden, H. (1973). Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP). Hydraulic Engineering Reports,. Available at: https://repository.tudelft.nl/islandora/object/uuid%3Af204e188-13b9-49d8-a6dc-4fb7c20562fc
Hasselmann, K., Hasselmann, K., Bauer, E., Janssen, P., Komen, G., Bertotti, L., Lionello, P., Guillaume, A., Cardone, V., Greenwood, J., Reistad, M., Zambresky, L., Ewing, J. (1988). The WAM model - a third generation ocean wave prediction model. Journal of Physical Oceanography, 18, 1775-1810.
Hasselmann, S., Hasselmann, K., Allender, J. H., and Barnett, T. P. (1985). Computations and parameterizations of the nonlinear energy transfer in a gravity wave spectrum, II, Parameterizations of the nonlinear energy transfer for application in wave models. Journal of Physical Oceanography, 15, 1378-1391.
Hasselmann, K. (1997). Multi-pattern fingerprint method for detection and attribution of climate change. Climate Dynamics, 13, 601-611, https://doi.org/10.1007/s003820050185
Hasselmann, K., Chapron, B., Aouf, L., Ardhuin, F., Collard, F., Engen, G., Hasselmann, S., Heimbach, P., Janssen, P., Johnsen, H., et al. (2013). The ERS SAR wave mode: A breakthrough in global ocean wave observations. In: “ERS Missions: 20 Years of Observing Earth”, 1st ed.; Fletcher, K., Ed.; European Space Agency: Noordwijk, The Netherlands, 2013; pp. 165-198.
Herman, A., Kaiser, R., Niemeyer, H.D. (2009). Wind-wave variability in shallow tidal sea - spectral modelling combined with neural network methods. Coastal Engineering, 56(7), 759-772, https://doi.org/10.1016/j.coastaleng.2009.02.007
Hersbach H. (2000). Decomposition of the continuous ranked probability score for ensemble prediction systems. Weather and Forecasting, 5(15), 1697-1709, https://doi.org/10.1175/WAF-D-16-0164.1
Hewitt, J. E, Cummings, V. J., Elis, J. I., Funnell, G., Norkko, A., Talley, T.S., Thrush, S.F. (2003). The role of waves in the colonisation of terrestrial sediments deposited in the marine environment. Journal of Experimental Marine Biology and Ecology, 290, 19-47, https://doi.org/10.1016/S0022-0981(03)00051-0
Higuera, P., Lara, L. J., Losada, I.J. (2014a). Three-dimensional interaction of waves and porous coastal structures using OpenFOAM®. Part I: Formulation and validation. Coastal Engineering, 83, 243-258, https://doi.org/10.1016/j.coastaleng.2013.08.010
Higuera, P., Lara, L. J., Losada, I.J. (2014b). Three-dimensional interaction of waves and porous coastal structures using OpenFOAM®. Part II: Application. Coastal Engineering, 83, 259-270, https://doi.org/10.1016/j.coastaleng.2013.09.002
Holthuijsen, L.H. (2007). Waves in Oceanic and Coastal Waters. Cambridge University Press, https://doi.org/10.1017/CBO9780511618536
Iafrati, A., Babanin, A.V., Onorato, M. (2013). Modulational instability, wave breaking and formation of large scale dipoles. Physical Review Letters, 110, 184504, : https://doi.org/10.1103/PhysRevLett.110.184504
Janssen, P.A.E.M (1989). Wave-induced stress and the drag of air flow over sea waves. Journal of Physical Oceanography, 19(6), 745-754, https://doi.org/10.1175/1520-0485(1989)019<0745:WISATD>2.0.CO;2
Janssen, P.A.E.M (1991). Quasi-linear theory of wind wave generation applied to wave forecasting. Journal of Physical Oceanography, 21, 1631-1642.
Janssen, P.A.E.M. (2004). The Interaction of Ocean Waves and Wind. Cambridge University Press, 308 p.
Janssen, P.A.E.M. (2012). Ocean wave effects on the daily cycle in SST. Journal of Geophysical Research: Oceans, 117, C00J32, https://doi.org/10.1029/2012JC007943
Janssen, P.A.E.M., Lionello, P., Reistad, M. and Hollingsworth, A. (1989). Hindcasts and data assimilation studies with the WAM model during the Seasat period. Journal of Geophysical Research: Oceans, C94, 973-993.
Janssen, P.A.E.M., Abdalla, S., Hersbach, H., Bidlot, J.R. (2007). Error estimation of buoy, satellite, and model wave height data. Journal of Atmospheric and Oceanic Technology, 24:1665-1677, https://doi.org/10.1175/JTECH2069.1
Kalra, R., Deo, M.C., Kumar, R., Agarwal, V.K. (2005). Artificial neural network to translate offshore satellite waves to data to coastal locations. Ocean Engineering, 32, 1917-1932, https://doi.org/10.1016/j.oceaneng.2005.01.007
Kirby, J., Dalrymple, R. (1983). Propagation of weakly nonlinear surface waves in the presence of varying depth and current. In: Proceedings of the 20th Congress, Int. Assoc. Hydraul. Res.(IAHR), Moscow, 1983, Paper S.1.5.3, pp. 198-202.
Komen, G.J., Hasselmann, K., and Hasselmann, S. (1984). On the existence of a fully developed windsea spectrum. Journal of Physical Oceanography, 14, 1271-1285.
Koutitas, C. G. (1990). Mathematical models in coastal engineering. Applied Ocean Research, 12(1), 52, https://doi.org/10.1016/S0141-1187(05)80022-7
Kudryavtsev, V.N., Makin, V.K., and Meirink, J.F. (2001). Simplified model of air flow above the waves. Boundary Layer Meteorology, 100, 63-90, https://doi.org/10.1023/A:1018914113697
Lalaurette, F. (2003). Early detection of abnormal weather conditions using a probabilistic extreme forecast index. Quarterly Journal of the Royal Meteorological Society, 129, 3037-3057, https://doi.org/10.1256/qj.02.152
Lara, J.L., Garcia, N., Losada, I.J. (2006). RANS modelling applied to random wave interaction with submerged permeable structures. Coastal Engineering, 53(5-6), 395-417, https://doi.org/10.1016/j.coastaleng.2005.11.003
Law Chune, S., Aouf, L. (2018). Wave effects in global ocean modeling: parametrizations vs. forcing from a wave model. Ocean Dynamics, 68, 1739-1758, https://doi.org/10.1007/s10236-018-1220-2
Le Traon, P.Y., Reppucci, A., Alvarez Fanjul, E., Aouf, L., Behrens, A., Belmonte, M., Bentamy, A., Bertino, L., Brando, V.E., Kreiner, M.B., Benkiran, M., Carval, T., Ciliberti, S.A., Claustre, H., Clementi, E., Coppini, G., Cossarini, G., De Alfonso Alonso-Muñoyerro, M., Delamarche, A., Dibarboure, G., Dinessen, F., Drevillon, M., Drillet, Y., Faugere, Y., Fernández, V., Fleming, A., Garcia-Hermosa, M.I., Sotillo, M.G., Garric, G., Gasparin, F., Giordan, C., Gehlen, M., Gregoire, M.L., Guinehut, S., Hamon, M., Harris, C., Hernandez, F., Hinkler, J.B., Hoyer, J., Karvonen, J., Kay, S., King, R., Lavergne, T., Lemieux-Dudon, B., Lima, L., Mao, C., Martin, M.J., Masina, S., Melet, A., Buongiorno Nardelli, B., Nolan, G., Pascual, A., Pistoia, J., Palazov, A., Piolle, J.F., Pujol, M.I., Pequignet, A.C., Peneva, E., Pérez Gómez, B., Petit de la Villeon, L., Pinardi, N., Pisano, A., Pouliquen, S., Reid, R., Remy, E., Santoleri, R., Siddorn, J., She, J., Staneva, J., Stoffelen, A., Tonani, M., Vandenbulcke, L., von Schuckmann, K., Volpe, G., Wettre, C.. and Zacharioudaki, A. (2019). From Observation to Information and Users: The Copernicus Marine Service Perspective. Frontiers in Marine Science, 6, 23, https://doi.org/10.3389/fmars.2019.00234
Lin, P. (2008). Numerical modeling of water waves (1st ed.). New York: Taylor and Francis.
Lionello, P., Gunther, H., and Janssen, P.A.E M. (1992). Assimilation of altimeter data in a global third generation wave model. Journal of Geophysical Research: Oceans, C97, 14453-14474, https://doi.org/10.1029/92JC01055
Madsen, P. A., and Larsen, J. (1987). An efficient finite-difference approach to the mild-slope equation. Coastal Engineering, 11, 329-351, https://doi.org/10.1016/0378-3839(87)90032-9
Marti F., Cazenave, A., Birol, F., Passaro, M., Léger, F., Niño, F., Almar, R., Benveniste, J., Legeais, J.F. (2021). Altimetry-based sea level trends along the coasts of Western Africa. Advances in Space Research, 68(2), 504-522, https://doi.org/10.1016/j.asr.2019.05.033
Maza, M., Lara, J. L., Losada, I. J. (2016). Solitary wave attenuation by vegetation patches. Advances in Water Resources, 98, 159-172, https://doi.org/10.1016/j.advwatres.2016.10.021
McCowan, J. (1894). On the Highest Waves of a Permanent Type. Philosophical Magazine, Edinburgh 38, 351-358.
Losada, I.J., Lara, J.L., Guanche, R., Gonzalez-Ondina, J.M. (2008). Numerical analysis of wave overtopping of rubble mound breakwaters. Coastal Engineering, 55, 47-62, https://doi.org/10.1016/j.coastaleng.2007.06.003
Mitsuyasu, H. (1970). On the growth of the spectrum of wind-generated waves. Coastal Engineering in Japan, 13(1), 1-14, https://doi.org/10.1080/05785634.1970.11924105
Mittermaier M. P., Csima, G. (2017). Ensemble versus deterministic Performance at kilometric scale. Weather and Forecasting, 32(5), https://doi.org/10.1175/WAF-D-16-0164.1
Molteni, F., Buizza, R., Palmer, T.N., Petroliagis, T. (1996). The ECMWF ensemble prediction system: methodology and validation. Quarterly Journal of the Royal Meteorological Society, 122(529), 73-119, https://doi.org/10.1002/qj.49712252905
Munk, W. H. (1950). Origin and generation of waves. Coastal Engineering Proceedings, 1, https://doi.org/10.9753/icce.v1.1
National Centers for Environmental Prediction (2012). Output fields from the NOAA WAVEWATCH III® wave model monthly hindcasts. NOAA National Centers for Environmental Information. Dataset.
Parkinson, C. L., and Cavalieri, D. J. (2012). Antarctic Sea ice variability and trends, 1979-2010. The Cryosphere, 6, 881–889, https://doi.org/10.5194/tc-6-881-2012
Pérez, B., Álvarez Fanjul, E., Pérez, S., de Alfonso, M., Vela, J. (2013). Use of tide gauge data in operational oceanography and sea level hazard warning systems, Journal of Operational Oceanography, 6(2), 1-18, https://doi.org/10.1080/1755876X.2013.11020147
Perez, J., Menendez, M., and Losada, I. J. (2017). GOW2: A global wave hindcast for coastal applications. Coastal Engineering, 124, 1-11, https://doi.org/10.1016/j.coastaleng.2017.03.005
Petroliagis, T.I., and Pinson, P. (2012). Early warnings of extreme winds using the ECMWF Extreme Forecast Index. Meteorological Applications, 21(2), 171-185, https://doi.org/10.1002/met.1339
Pezzutto P., Saulter A., Cavaleri L., Bunney, C., Marcucci, F., Sebastianelli, S. (2016). Performance comparison of meso-scale ensemble wave forecasting systems for Mediterranean Sea states. Ocean Modelling, 104, 171-186, https://doi.org/10.1016/j.ocemod.2016.06.002
Rascle N., Ardhuin, F., Queffeulou, P., Croizé-Fillon, D. (2008). A global wave parameter database for geophysical applications. Part 1: Wave-current–turbulence interaction parameters for the open ocean based on traditional parameterizations. Ocean Modelling, 25(3-4), 154-171, doi:10.1016/j.ocemod.2008.07.006
Reguero, B.G., Menéndez, M., Méndez, F.J., Mínguez, R., Losada, I.J. (2012). A global Ocean Wave (GOW) calibrated reanalysis from 1948 onwards. Coastal Engineering, 65, 38-55, https://doi.org/10.1016/j.coastaleng.2012.03.003
Ribal, A., Young, I.R. (2019). 33 years of globally calibrated wave height and wind speed data based on altimeter observations. Scientific Data, 6, 77, https://doi.org/10.1038/s41597-019-0083-9
Rusu, L., Pilar, P., Guedes Soares, C. (2008). Hindcast of the wave conditions along the west Iberian coast. Coastal Engineering, 55(11), 906-919, https://doi.org/10.1016/j.coastaleng.2008.02.029
Saetra, O., and Bidlot, J.-R. (2004). Potential benefit of using probabilistic forecasts for waves and marine winds based on the ECMWF ensemble prediction system. Weather and Forecasting, 19(4), 673-689, https://doi.org/10.1175/1520-0434(2004)019<0673:PBOUPF>2.0.CO;2
Saha, S., Moorthi, S., Pan, H.-L., Wu, X., Wang, J., Nadiga, S., … Goldberg, M. (2010). The NCEP Climate Forecast System Reanalysis. Bulletin of the American Meteorological Society, 91(8), 1015-1057, https://doi.org/10.1175/2010BAMS3001.1
Saulter A. N., Bunney, C., King, R., Water, J. (2020). An Application of NEMOVAR for Regional Wave Model Data Assimilation, Frontiers in Marine Science, 7, 579834, https://doi.org/10.3389/fmars.2020.579834
Shapiro, R. (1970). Smoothing filtering and boundary effects. Reviews of Geophysics, 8(2), 359-387, https://doi.org/10.1029/RG008i002p00359
State of the Global Climate 2020 (WMO-No. 1264).
Staneva, J., Alari, V., Breivik, Ø. et al. (2017). Effects of wave-induced forcing on a circulation model of the North Sea. Ocean Dynamics, 67, 81-101, https://doi.org/10.1007/s10236-016-1009-0
Staneva, J., Grayek, S., Behrens, A., and Günther, H. (2021). GCOAST: skill assessments of coupling wave and circulation models (NEMO-WAM). Journal of Physics: Conference Series, 1730, 012071. doi:10.1088/1742-6596/1730/1/012071
Stansby, P., Zhou, J., Kuang, C., Walkden, M., Hall, J., Dickson, M. (2007). Long-term prediction of nearshore wave climate with an application to cliff erosion. In: McKee Smith, Jane (Ed.), Proc. of International Conference Coastal Engineering, ASCE, pp. 616-627.
Stopa, J.E. (2018). Wind forcing calibration and wave hindcast comparison using multiple reanalysis and merged satellite wind datasets. Ocean Modelling, 127, 55-69, https://doi.org/10.1016/j.ocemod.2018.04.008
Swail, V., Jensen, R., Lee, B., Turton, J., Thomas, J., Gulev, S., Yelland, M., Etala, P., Meldrum, D., Birkemeier, W., Burnett, W., Warren, G. (2010). Wave Measurements, Needs and Developments for the Next Decade. Proceedings of OceanObs’09: Sustained Ocean Observations and Information for Society Conference (Volume 2), Venice, Italy, 21-25 September 2009 (J. Hall, D.E. Harrison and D. Stammer, eds.). ESA Publication WPP-306.
Thomson, J., Ackley, S., Girard-Ardhuin, F., Ardhuin, F., Babanin, A.V., Boutin, G., Brozena, J., Cheng, S., Collins, C., Doble, M., Fairall, C., Guest, P., Gebhardt, C., Gemmrich, J., Graber, H.C., Holt, B., Lehner, S., Lund, B., Meylan, M.H., Maksym, T., Montiel, F., Perrie, W., Persson, O., Rainville, L., Rogers, W.E., Shen, H., Shen, H., Squire, V., Stammerjohn, S., Stopa, J., Smith, M.M., Sutherland, P., Wadhams, P. (2018). Overview of the Arctic Sea State and Boundary Layer Physics Program. Journal of Geophysical Research: Oceans, 123(12), 8674-8687, https://doi.org/10.1002/2018JC013766
Tolman, H. L. (1989). The numerical model WAVEWATCH: a third generation model for the hindcasting of wind waves on tides in shelf seas. Communications on Hydraulic and Geotechnical Engineering, Delft Univ. of Techn., ISSN 0169-6548, Rep. no. 89-2, 72 pp.
Tolman, H.L. (2010). WAVEWATCH III development best practices. Camp Springs.
Tolman H.L., and the WAVEWATCH III® Development Group (2014). User Manual and System Documentation of WAVEWATCH III® version 4.18. Technical Note 316, NOAA/NWS/NCEP/MMAB. Available at: https://polar.ncep.noaa.gov/waves/wavewatch/manual.v4.18.pdf
Thomas, A., Mendez, F. J., and Losada, I. J. (2008). A method for spatial calibration of wave hindcast data bases. Continental Shelf Research, 28(3), 391-398, https://doi.org/10.1016/j.csr.2007.09.009
Trulsen, K. C., Nieto Borge, J., Gramstad, O., Aouf, L., and Lefèvre, J.-M. (2015). Crossing sea state and rogue wave probability during the Prestige accident. Journal of Geophysical Research: Oceans, 120, 7113-7136, https://doi.org/10.1002/2015JC011161
Tsagareli, K.N., Babanin, A.V., Walker, D.J., and Young, I.R. (2010). Numerical investigation of spectral evolution of wind waves. Part 1. Wind input source function. Journal of Physical Oceanography, 40(4), 656-666, https://doi.org/10.1175/2009JPO4370.1
Tsay, T. K., Zhu, W., and Liu, P. L.-F. (1989) A finite element model for wave refraction, diffraction, reflection and dissipation. Applied Ocean Research, 11, 33-38, https://doi.org/10.1016/0141-1187(89)90005-9
Van der Meer, J., Allsop, W., Bruce, T., Rouck, J., Kortenhaus, A., Pullen, T., Schüttrumpf, H., Troch, P., Zanuttigh, B. (2016). EurOtop: Manual on wave overtopping of sea defences and related structures - An overtopping manual largely based on European research, but for worldwide application, 2nd edition.
Van der Ven, P., Reijmerink, B., Van der Hout, A., De Jong, M. (2018). Comparison of Validation Studies of Wave - Penetration Models using Open Benchmark Datasets of Deltares, PIANC World Congress 2018, At Panama City, Panama.
Veron, F. (2015). Ocean spray. Annual Review of Fluid Mechanics, 47, 507-538, https://doi.org/10.1146/annurev-fluid-010814-014651
Visbeck, M. (2018). Ocean science research is key for a sustainable future. Nature Communication, 9, 690, https://doi.org/10.1038/s41467-018-03158-3
Voorrips, A. C., Makin V. K., and Hasselmann S. (1997). Assimilation of wave spectra from pitch-and-roll buoys in a North Sea wave model. Journal of Geophysical Research: Oceans, 102, 5829-5849, https://doi.org/10.1029/96JC03242
WAMDI group (The) (1988). The WAM Model - A Third Generation Ocean Wave Prediction Model. Journal of Physical Oceanography, 18, 1775-1810, https://doi.org/10.1175/1520-0485(1988)018<1775:TWMTGO>2.0.CO;2
Wang, J. K., Aouf, L., Dalphinet, A., Zhang, Y. G., Xu, Y., Hauser, D., Liu, J. Q. (2021). The Wide Swath Significant Wave Height: An Innovative Reconstruction of Significant Wave Heights From CFOSAT’s SWIM and Scatterometer Using Deep Learning. Geophysical Research Lettera, 48(6), https://doi.org/10.1029/2020GL091276
Wilby, R. and Dessai, S. (2010). Robust adaptation to climate change. Weather, 65, 180-185, https://doi.org/10.1002/wea.543
Young, I.R. (1999). Wind Generated Ocean Waves, Elsevier, Amsterdam, 288 p.
Zakharov, V.E. (1968). Stability of periodic waves of finite amplitude on the surface of a deep fluid. Journal of Applied Mechanics and Technical Physics, 9(2), 190-194
Zieger, S., Greenslade, D.J.M., and Kepert, J.D. (2018). Wave ensemble forecast system for tropical cyclones in the Australian region. Ocean Dynamics, 68(4-5):603-625, https://doi.org/10.1007/s10236-018-1145-9
Zijlema, M. (2009). Parallel, unstructured mesh implementation for SWAN. Proceedings of the Coastal Engineering Conference. 470-482, https://doi.org/10.1142/9789814277426_0040
Zijlema, M., Stelling, G., and Smit, P. (2011). SWASH: An operational public domain code for simulating wave fields and rapidly varied flows in coastal waters. Coastal Engineering, 58, 992-1012, https://doi.org/10.1016/j.coastaleng.2011.05.015
To start contributing, sharing knowledge and editing the WIKI, please login !


Follow us